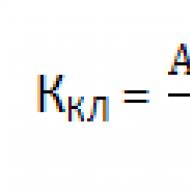
Система линейных уравнений основные определения. Система линейных алгебраических уравнений. Способ решения введением новой переменной

Содержание урока

Линейные уравнения с двумя переменными

У школьника имеется 200 рублей, чтобы пообедать в школе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе можно накупить на 200 рублей?

Обозначим количество пирожных через x , а количество чашек кофе через y . Тогда стоимость пирожных будет обозначаться через выражение 25x , а стоимость чашек кофе через 10y .

25x — стоимость x пирожных
10y — стоимость y чашек кофе

Итоговая сумма должна равняться 200 рублей. Тогда получится уравнение с двумя переменными x и y

25x + 10y = 200

Сколько корней имеет данное уравнение?

Всё зависит от аппетита школьника. Если он купит 6 пирожных и 5 чашек кофе, то корнями уравнения будут числа 6 и 5.

Говорят, что пара значений 6 и 5 являются корнями уравнения 25x + 10y = 200 . Записывается как (6; 5) , при этом первое число является значением переменной x , а второе — значением переменной y .

6 и 5 не единственные корни, которые обращают уравнение 25x + 10y = 200 в тождество. При желании на те же 200 рублей школьник может купить 4 пирожных и 10 чашек кофе:

В этом случае корнями уравнения 25x + 10y = 200 является пара значений (4; 10) .

Более того, школьник может вообще не покупать кофе, а купить пирожные на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 8 и 0

Или наоборот, не покупать пирожные, а купить кофе на все 200 рублей. Тогда корнями уравнения 25x + 10y = 200 будут значения 0 и 20

Попробуем перечислить все возможные корни уравнения 25x + 10y = 200 . Условимся, что значения x и y принадлежат множеству целых чисел. И пусть эти значения будут бóльшими или равными нулю:

x ∈ Z, y ∈ Z;
x ≥ 0, y ≥ 0

Так будет удобно и самому школьнику. Пирожные удобнее покупать целыми, чем к примеру несколько целых пирожных и половину пирожного. Кофе также удобнее брать целыми чашками, чем к примеру несколько целых чашек и половину чашки.

Заметим, что при нечетном x невозможно достичь равенства ни при каком y . Тогда значениями x будут следующие числа 0, 2, 4, 6, 8. А зная x можно без труда определить y

Таким образом, мы получили следующие пары значений (0; 20), (2; 15), (4; 10), (6; 5), (8; 0). Эти пары являются решениями или корнями уравнения 25x + 10y = 200 .Они обращают данное уравнение в тождество.

Уравнение вида ax + by = c называют линейным уравнением с двумя переменными . Решением или корнями этого уравнения называют пару значений (x; y ), которая обращает его в тождество.

Отметим также, что если линейное уравнение с двумя переменными записано в виде ax + b y = c , то говорят, что оно записано в каноническом (нормальном) виде.

Некоторые линейные уравнения с двумя переменными могут быть приведены к каноническому виду.

Например, уравнение 2(16x + 3y − 4) = 2(12 + 8x − y ) можно привести к виду ax + by = c . Раскроем скобки в обеих частях этого уравнения, получим 32x + 6y − 8 = 24 + 16x − 2y . Слагаемые, содержащие неизвестные сгруппируем в левой части уравнения, а слагаемые свободные от неизвестных — в правой. Тогда получим 32x − 16x + 6y + 2y = 24 + 8 . Приведём подобные слагаемые в обеих частях, получим уравнение 16x + 8y = 32. Это уравнение приведено к виду ax + by = c и является каноническим.

Рассмотренное ранее уравнение 25x + 10y = 200 также является линейным уравнением с двумя переменными в каноническом виде. В этом уравнении параметры a , b и c равны значениям 25, 10 и 200 соответственно.

На самом деле уравнение ax + by = c имеет бесчисленное множество решений. Решая уравнение 25x + 10y = 200, мы искали его корни толькона множестве целых чисел. В результате получили несколько пар значений, которые обращали данное уравнение в тождество. Но на множестве рациональных чисел уравнение 25x + 10y = 200 будет иметь бесчисленное множество решений.

Для получения новых пар значений, нужно взять произвольное значение для x , затем выразить y . К примеру, возьмем для переменной x значение 7. Тогда получим уравнение с одной переменной 25 × 7 + 10y = 200 в котором можно выразить y

Пусть x = 15 . Тогда уравнение 25x + 10y = 200 примет вид 25 × 15 + 10y = 200. Отсюда находим, что y = −17,5

Пусть x = −3 . Тогда уравнение 25x + 10y = 200 примет вид 25 × (−3) + 10y = 200. Отсюда находим, что y = −27,5

Система двух линейных уравнений с двумя переменными

Для уравнения ax + by = c можно сколько угодно раз брать произвольные значение для x и находить значения для y . Отдельно взятое такое уравнение будет иметь бесчисленное множество решений.

Но бывает и так, что переменные x и y связаны не одним, а двумя уравнениями. В этом случае они образуют так называемую систему линейных уравнений с двумя переменными . Такая система уравнений может иметь одну пару значений (или по-другому: «одно решение»).

Может случиться и так, что система вовсе не имеет решений. Бесчисленное множество решений система линейных уравнений может иметь в редких и в исключительных случаях.

Два линейных уравнения образуют систему тогда, когда значения x и y входят в каждое из этих уравнений.

Вернемся к самому первому уравнению 25x + 10y = 200 . Одной из пар значений для этого уравнения была пара (6; 5) . Это случай, когда на 200 рублей можно можно было купить 6 пирожных и 5 чашек кофе.

Составим задачу так, чтобы пара (6; 5) стала единственным решением для уравнения 25x + 10y = 200 . Для этого составим ещё одно уравнение, которое связывало бы те же x пирожных и y чашечек кофе.

Поставим текст задачи следующим образом:

«Школьник купил на 200 рублей несколько пирожных и несколько чашек кофе. Пирожное стоит 25 рублей, а чашка кофе 10 рублей. Сколько пирожных и чашек кофе купил школьник, если известно что количество пирожных на одну единицу больше количества чашек кофе?»

Первое уравнение у нас уже есть. Это уравнение 25x + 10y = 200 . Теперь составим уравнение к условию «количество пирожных на одну единицу больше количества чашек кофе» .

Количество пирожных это x , а количество чашек кофе это y . Можно записать эту фразу с помощью уравнения x − y = 1. Это уравнение будет означать, что разница между пирожными и кофе составляет 1.

x = y + 1 . Это уравнение означает, что количество пирожных на единицу больше, чем количество чашек кофе. Поэтому для получения равенства, к количеству чашек кофе прибавлена единица. Это легко можно понять, если воспользоваться моделью весов, которые мы рассматривали при изучении простейших задач:

Получили два уравнения: 25x + 10y = 200 и x = y + 1. Поскольку значения x и y , а именно 6 и 5 входят в каждое из этих уравнений, то вместе они образуют систему. Запишем эту систему. Если уравнения образуют систему, то они обрамляются знаком системы. Знак системы это фигурная скобка:

Давайте решим данную систему. Это позволит увидеть, как мы придём к значениям 6 и 5. Существует много методов решения таких систем. Рассмотрим наиболее популярные из них.

Метод подстановки

Название этого метода говорит само за себя. Суть его заключается в том, чтобы одно уравнение подставить в другое, предварительно выразив одну из переменных.

В нашей системе ничего выражать не нужно. Во втором уравнении x = y + 1 переменная x уже выражена. Эта переменная равна выражению y + 1 . Тогда можно подставить это выражение в первое уравнение вместо переменной x

После подстановки выражения y + 1 в первое уравнение вместо x , получим уравнение 25(y + 1) + 10y = 200 . Это линейное уравнение с одной переменной. Такое уравнение решить довольно просто:

Мы нашли значение переменной y . Теперь подставим это значение в одно из уравнений и найдём значение x . Для этого удобно использовать второе уравнение x = y + 1 . В него и подставим значение y

Значит пара (6; 5) является решением системы уравнений, как мы и задумывали. Выполняем проверку и убеждаемся, что пара (6; 5) удовлетворяет системе:

Пример 2

Подставим первое уравнение x = 2 + y во второе уравнение 3x − 2y = 9 . В первом уравнении переменная x равна выражению 2 + y . Это выражение и подставим во второе уравнение вместо x

Теперь найдём значение x . Для этого подставим значение y в первое уравнение x = 2 + y

Значит решением системы является пара значение (5; 3)

Пример 3 . Решить методом подстановки следующую систему уравнений:

Здесь в отличие от предыдущих примеров, одна из переменных не выражена явно.

Чтобы подставить одно уравнение в другое, сначала нужно .

Выражать желательно ту переменную, которая имеет коэффициент единицу. Коэффициент единицу имеет переменная x , которая содержится в первом уравнении x + 2y = 11 . Эту переменную и выразим.

После выражения переменной x , наша система примет следующий вид:

Теперь подставим первое уравнение во второе и найдем значение y

Подставим y x

Значит решением системы является пара значений (3; 4)

Конечно, выражать можно и переменную y . Корни от этого не изменятся. Но если выразить y, получится не очень-то и простое уравнение, на решение которого уйдет больше времени. Выглядеть это будет следующим образом:

Видим, что в данном примере выражать x намного удобнее, чем выражать y .

Пример 4 . Решить методом подстановки следующую систему уравнений:

Выразим в первом уравнении x . Тогда система примет вид:

Подставим y в первое уравнение и найдём x . Можно воспользоваться изначальным уравнением 7x + 9y = 8 , либо воспользоваться уравнением , в котором выражена переменная x . Этим уравнением и воспользуемся, поскольку это удобно:

Значит решением системы является пара значений (5; −3)

Метод сложения

Метод сложения заключается в том, чтобы почленно сложить уравнения, входящие в систему. Это сложение приводит к тому, что образуется новое уравнение с одной переменной. А решить такое уравнение довольно просто.

Решим следующую систему уравнений:

Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. Получим следующее равенство:

Приведем подобные слагаемые:

В результате получили простейшее уравнение 3x = 27 корень которого равен 9. Зная значение x можно найти значение y . Подставим значение x во второе уравнение x − y = 3 . Получим 9 − y = 3 . Отсюда y = 6 .

Значит решением системы является пара значений (9; 6)

Пример 2

Сложим левую часть первого уравнения с левой частью второго уравнения. А правую часть первого уравнения с правой частью второго уравнения. В получившемся равенстве приведем подобные слагаемые:

В результате получили простейшее уравнение 5x = 20, корень которого равен 4. Зная значение x можно найти значение y . Подставим значение x в первое уравнение 2x + y = 11 . Получим 8 + y = 11 . Отсюда y = 3 .

Значит решением системы является пара значений (4;3)

Процесс сложения подробно не расписывают. Его нужно выполнять в уме. При сложении оба уравнения должны быть приведены к каноническому виду. То есть к виду ac + by = c .

Из рассмотренных примеров видно, что основная цель сложения уравнений это избавление от одной из переменных. Но не всегда удаётся сразу решить систему уравнений методом сложения. Чаще всего систему предварительно приводят к виду, при котором можно сложить уравнения, входящие в эту систему.

Например, систему можно сразу решить методом сложения. При сложении обоих уравнений, слагаемые y и −y исчезнут, поскольку их сумма равна нулю. В результате образуется простейшее уравнение 11x = 22 , корень которого равен 2. Затем можно будет определить y равный 5.

А систему уравнений методом сложения сразу решить нельзя, поскольку это не приведёт к исчезновению одной из переменных. Сложение приведет к тому, что образуется уравнение 8x + y = 28 , имеющее бесчисленное множество решений.

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение равносильное данному. Это правило справедливо и для системы линейных уравнений с двумя переменными. Одно из уравнений (или оба уравнения) можно умножить на какое-нибудь число. В результате получится равносильная система, корни которой будут совпадать с предыдущей.

Вернемся к самой первой системе , которая описывала сколько пирожных и чашек кофе купил школьник. Решением этой системы являлась пара значений (6; 5) .

Умножим оба уравнения, входящие в эту систему на какие-нибудь числа. Скажем первое уравнение умножим на 2, а второе на 3

В результате получили систему
Решением этой системы по-прежнему является пара значений (6; 5)

Это значит, что уравнения входящие в систему можно привести к виду, пригодному для применения метода сложения.

Вернемся к системе , которую мы не смогли решить методом сложения.

Умножим первое уравнение на 6, а второе на −2

Тогда получим следующую систему:

Сложим уравнения, входящие в эту систему. Сложение компонентов 12x и −12x даст в результате 0, сложение 18y и 4y даст 22y , а сложение 108 и −20 даст 88. Тогда получится уравнение 22y = 88 , отсюда y = 4 .

Если первое время тяжело складывать уравнения в уме, то можно записывать как складывается левая часть первого уравнения с левой частью второго уравнения, а правая часть первого уравнения с правой частью второго уравнения:

Зная, что значение переменной y равно 4, можно найти значение x . Подставим y в одно из уравнений, например в первое уравнение 2x + 3y = 18 . Тогда получим уравнение с одной переменной 2x + 12 = 18 . Перенесем 12 в правую часть, изменив знак, получим 2x = 6 , отсюда x = 3 .

Пример 4 . Решить следующую систему уравнений методом сложения:

Умножим второе уравнение на −1. Тогда система примет следующий вид:

Сложим оба уравнения. Сложение компонентов x и −x даст в результате 0, сложение 5y и 3y даст 8y , а сложение 7 и 1 даст 8. В результате получится уравнение 8y = 8 , корень которого равен 1. Зная, что значение y равно 1, можно найти значение x .

Подставим y в первое уравнение, получим x + 5 = 7 , отсюда x = 2

Пример 5 . Решить следующую систему уравнений методом сложения:

Желательно, чтобы слагаемые содержащие одинаковые переменные, располагались друг под другом. Поэтому во втором уравнении слагаемые 5y и −2x поменяем местами. В результате система примет вид:

Умножим второе уравнение на 3. Тогда система примет вид:

Теперь сложим оба уравнения. В результате сложения получим уравнение 8y = 16 , корень которого равен 2.

Подставим y в первое уравнение, получим 6x − 14 = 40 . Перенесем слагаемое −14 в правую часть, изменив знак, получим 6x = 54 . Отсюда x = 9.

Пример 6 . Решить следующую систему уравнений методом сложения:

Избавимся от дробей. Умножим первое уравнение на 36, а второе на 12

В получившейся системе первое уравнение можно умножить на −5, а второе на 8

Сложим уравнения в получившейся системе. Тогда получим простейшее уравнение −13y = −156 . Отсюда y = 12 . Подставим y в первое уравнение и найдем x

Пример 7 . Решить следующую систему уравнений методом сложения:

Приведем оба уравнения к нормальному виду. Здесь удобно применить правило пропорции в обоих уравнениях. Если в первом уравнении правую часть представить как , а правую часть второго уравнения как , то система примет вид:

У нас получилась пропорция. Перемножим её крайние и средние члены. Тогда система примет вид:

Первое уравнение умножим на −3, а во втором раскроем скобки:

Теперь сложим оба уравнения. В результате сложения этих уравнений, мы получим равенство, в обеих частях которого будет ноль:

Получается, что система имеет бесчисленное множество решений.

Но мы не можем просто так взять с неба произвольные значения для x и y . Мы можем указать одно из значений, а другое определится в зависимости от значения, указанного нами. Например, пусть x = 2 . Подставим это значение в систему:

В результате решения одного из уравнений, определится значение для y , которое будет удовлетворять обоим уравнениям:

Получившаяся пара значений (2; −2) будет удовлетворять системе:

Найдём еще одну пару значений. Пусть x = 4. Подставим это значение в систему:

На глаз можно определить, что значение y равно нулю. Тогда получим пару значений (4; 0), которая удовлетворяет нашей системе:

Пример 8 . Решить следующую систему уравнений методом сложения:

Умножим первое уравнение на 6, а второе на 12

Перепишем то, что осталось:

Первое уравнение умножим на −1. Тогда система примет вид:

Теперь сложим оба уравнения. В результате сложения образуется уравнение 6b = 48 , корень которого равен 8. Подставим b в первое уравнение и найдём a

Система линейных уравнений с тремя переменными

В линейное уравнение с тремя переменными входит три переменные с коэффициентами, а также свободный член. В каноническом виде его можно записать следующим образом:

ax + by + cz = d

Данное уравнение имеет бесчисленное множество решений. Придавая двум переменным различные значения, можно найти третье значение. Решением в этом случае является тройка значений (x; y; z ) которая обращает уравнение в тождество.

Если переменные x, y, z связаны между собой тремя уравнениями, то образуется система трех линейных уравнений с тремя переменными. Для решения такой системы можно применять те же методы, которые применяются к линейным уравнениям с двумя переменными: метод подстановки и метод сложения.

Пример 1 . Решить следующую систему уравнений методом подстановки:

Выразим в третьем уравнении x . Тогда система примет вид:

Теперь выполним подстановку. Переменная x равна выражению 3 − 2y − 2z . Подставим это выражение в первое и второе уравнение:

Раскроем скобки в обоих уравнениях и приведём подобные слагаемые:

Мы пришли к системе линейных уравнений с двумя переменными. В данном случае удобно применить метод сложения. В результате переменная y исчезнет, и мы сможем найти значение переменной z

Теперь найдём значение y . Для этого удобно воспользоваться уравнением −y + z = 4. Подставим в него значение z

Теперь найдём значение x . Для этого удобно воспользоваться уравнением x = 3 − 2y − 2z . Подставим в него значения y и z

Таким образом, тройка значений (3; −2; 2) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:

Пример 2 . Решить систему методом сложения

Сложим первое уравнение со вторым, умноженным на −2.

Если второе уравнение умножить на −2, то оно примет вид −6x + 6y − 4z = −4 . Теперь сложим его с первым уравнением:

Видим, что в результате элементарных преобразований, определилось значение переменной x . Оно равно единице.

Вернемся к главной системе. Сложим второе уравнение с третьим, умноженным на −1. Если третье уравнение умножить на −1, то оно примет вид −4x + 5y − 2z = −1 . Теперь сложим его со вторым уравнением:

Получили уравнение x − 2y = −1 . Подставим в него значение x , которое мы находили ранее. Тогда мы сможем определить значение y

Теперь нам известны значения x и y . Это позволяет определить значение z . Воспользуемся одним из уравнений, входящим в систему:

Таким образом, тройка значений (1; 1; 1) является решением нашей системы. Проверкой убеждаемся, что эти значения удовлетворяют системе:

Задачи на составление систем линейных уравнений

Задача на составление систем уравнений решается путем ввода нескольких переменных. Далее составляются уравнения на основании условий задачи. Из составленных уравнений образуют систему и решают её. Решив систему, необходимо выполнить проверку на то, удовлетворяет ли её решение условиям задачи.

Задача 1 . Из города в колхоз выехала машина «Волга». Обратно она возвращалась по другой дороге, которая была на 5 км короче первой. Всего в оба конца машина проехала 35 км. Сколько километров составляет длина каждой дороги?

Решение

Пусть x — длина первой дороги, y — длина второй. Если в оба конца машина проехала 35 км, то первое уравнение можно записать как x + y = 35. Это уравнение описывает сумму длин обеих дорог.

Сказано, что обратно машина возвращалась по дороге которая была короче первой на 5 км. Тогда второе уравнение можно записать как x − y = 5. Это уравнение показывает, что разница между длинами дорог составляет 5 км.

Либо второе уравнение можно записать как x = y + 5 . Этим уравнением и воспользуемся.

Поскольку переменные x и y в обоих уравнениях обозначают одно и то же число, то мы можем образовать из них систему:

Решим эту систему каким-нибудь из изученных ранее методов. В данном случае удобно воспользоваться методом подстановки, поскольку во втором уравнении переменная x уже выражена.

Подставим второе уравнение в первое и найдём y

Подставим найденное значение y в во второе уравнение x = y + 5 и найдём x

Длина первой дороги была обозначена через переменную x . Теперь мы нашли её значение. Переменная x равна 20. Значит длина первой дороги составляет 20 км.

А длина второй дороги была обозначена через y . Значение этой переменной равно 15. Значит длина второй дороги составляет 15 км.

Выполним проверку. Для начала убедимся, что система решена правильно:

Теперь проверим удовлетворяет ли решение (20; 15) условиям задачи.

Было сказано, что всего в оба конца машина проехала 35 км. Складываем длины обеих дорог и убеждаемся, что решение (20; 15) удовлетворяет данному условию: 20 км + 15 км = 35 км

Следующее условие: обратно машина возвращалась по другой дороге, которая была на 5 км короче первой . Видим, что решение (20; 15) удовлетворяет и этому условию, поскольку 15 км короче, чем 20 км на 5 км: 20 км − 15 км = 5 км

При составлении системы важно, чтобы переменные обозначали одни и те же числа во всех уравнениях, входящих в эту систему.

Так наша система содержит два уравнения. Эти уравнения в свою очередь содержат переменные x и y , которые обозначают одни и те же числа в обоих уравнениях, а именно длины дорог, равных 20 км и 15 км.

Задача 2 . На платформу были погружены дубовые и сосновые шпалы, всего 300 шпал. Известно, что все дубовые шпалы весили на 1 т меньше, чем все сосновые. Определить, сколько было дубовых и сосновых шпал отдельно, если каждая дубовая шпала весила 46 кг, а каждая сосновая 28 кг.

Решение

Пусть x дубовых и y сосновых шпал было погружено на платформу. Если всего шпал было 300, то первое уравнение можно записать как x + y = 300 .

Все дубовые шпалы весили 46x кг, а сосновые весили 28y кг. Поскольку дубовые шпалы весили на 1 т меньше, чем сосновые, то второе уравнение можно записать, как 28y − 46x = 1000 . Это уравнение показывает, что разница масс между дубовыми и сосновыми шпалами, составляет 1000 кг.

Тонны были переведены в килограммы, поскольку масса дубовых и сосновых шпал измерена в килограммах.

В результате получаем два уравнения, которые образуют систему

Решим данную систему. Выразим в первом уравнении x . Тогда система примет вид:

Подставим первое уравнение во второе и найдём y

Подставим y в уравнение x = 300 − y и узнаем чему равно x

Значит на платформу было погружено 100 дубовых и 200 сосновых шпал.

Проверим удовлетворяет ли решение (100; 200) условиям задачи. Для начала убедимся, что система решена правильно:

Было сказано, что всего было 300 шпал. Складываем количество дубовых и сосновых шпал и убеждаемся, что решение (100; 200) удовлетворяет данному условию: 100 + 200 = 300.

Следующее условие: все дубовые шпалы весили на 1 т меньше, чем все сосновые . Видим, что решение (100; 200) удовлетворяет и этому условию, поскольку 46 × 100 кг дубовых шпал легче, чем 28 × 200 кг сосновых шпал: 5600 кг − 4600 кг = 1000 кг.

Задача 3 . Взяли три куска сплава меди с никелем в отношениях 2: 1 , 3: 1 и 5: 1 по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4: 1 . Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

В общем случае линейное уравнение имеет вид:

Уравнение имеет решение: если хотя бы один из коэффициентов при неизвестных отличен от нуля. В этом случае любой -мерный вектор называется решением уравнения, если при подстановке его координат уравнение обращается в тождество.

Общая характеристика разрешенной системы уравнений

Пример 20.1

Дать характеристику системе уравнений .

Решение :

1. Входит ли в состав противоречивое уравнение? (Если коэффициенты, в этом случае уравнение имеет вид: и называется противоречивым .)

Если система содержит противоречивое, то такая система несовместна и не имеет решения

2. Найти все разрешенные переменные . (Неизвестная называется разрешенной для системы уравнений, если она входит в одно из уравнений системы с коэффициентом +1, а в остальные уравнения не входит (т.е. входит с коэффициентом, равным нулю).

3. Является ли система уравнений разрешенной? (Система уравнений называется разрешенной , если каждое уравнение системы содержит разрешенную неизвестную, среди которых нет совпадающих)

Разрешенные неизвестные, взятые по одному из каждого уравнения системы, образуют полный набор разрешенных неизвестных системы. (в нашем примере это )

Разрешенные неизвестные, входящие в полный набор, называют также базисными (), а не входящие в набор — свободными ().

В общем случае разрешенная система уравнений имеет вид:

На данном этапе главное понять что такое разрешенная неизвестная (входящая в базис и свободная).

Общее Частное Базисное решения

Общим решением разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные:

Частным решением называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных.

Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.

Базисное решение (вектор) называется вырожденным , если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.
Базисное решение называется невырожденным , если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.

Теорема (1)

Разрешенная система уравнений всегда совместна (потому что она имеет хотя бы одно решение); причем если система не имеет свободных неизвестных, (то есть в системе уравнений все разрешенные входят в базис) то она определена (имеет единственное решение); если же имеется хотя бы одна свободная переменная, то система не определена (имеет бесконечное множество решений).

Пример 1. Найти общее, базисное и какое-либо частное решение системы уравнений:

Решение :

1. Проверяем является ли система разрешенной?

Система является разрешенной (т.к. каждое из уравнений содержит в себе разрешенную неизвестную)

2. Включаем в набор разрешенные неизвестные — по одному из каждого уравнения .

3. Записываем общее решение в зависимости от того какие разрешенные неизвестные мы включили в набор .

4. Находим частное решение . Для этого приравниваем свободные переменные, которые мы не включили в набор приравнять к произвольным числам.

Ответ: частное решение (один из вариантов)

5. Находим базисное решение . Для этого приравниваем свободные переменные, которые мы не включили в набор к нулю.

Элементарные преобразования линейных уравнений

Системы линейных уравнений приводятся к равносильным разрешенным системам с помощью элементарных преобразований.

Теорема (2)

Если какое-либо уравнение системы умножить на некоторое отличное от нуля число , а остальные уравнения оставить без изменения, то . (то есть если умножить левую и правую часть уравнения на одно и то же число то получится уравнение, равносильное данному)

Теорема (3)

Если к какому-либо уравнению системы прибавить другое , а все остальные уравнения оставить без изменения, то получится система, равносильная данной . (то есть если сложить два уравнения (сложив их левые и правые части) то получится уравнение равносильное данным)

Следствие из Теорем (2 и 3)

Если к какому-либо уравнению прибавить другое, умноженное на некоторое число , а все остальные уравнения оставить без изменения, то получится система, равносильная данной .

Формулы пересчета коэффициентов системы

Если у нас есть система уравнений и мы хотим преобразовать ее в разрешенную систему уравнений в этом нам поможет метод Жордана-Гаусса.

Преобразование Жордана с разрешающим элементом позволяет получить для системы уравнений разрешенную неизвестную в уравнении с номером . (пример 2).

Преобразование Жордана состоит из элементарных преобразований двух типов:

Допустим мы хотим сделать неизвестную в нижнем уравнении разрешенной неизвестной. Для этого мы должны разделить на , так чтобы сумма .

Пример 2 Пересчитаем коэффициенты системы

При делении уравнения с номером на , его коэффициенты пересчитываются по формулам:

Чтобы исключить из уравнения с номером , нужно уравнение с номером умножить на и прибавить к этому уравнению.

Теорема (4) О сокращении числа уравнений системы.

Если система уравнений содержит тривиальное уравнение, то его можно исключить из системы, при этом получится система равносильная исходной.

Теорема (5) О несовместимости системы уравнений.

Если система уравнений содержит противоречивое уравнение, то она несовместна.

Алгоритм метода Жордана-Гаусса

Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:

Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.
Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.
Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.
Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.
Далее заново переходят к пункту 1

Пример 3 Решить систему уравнений методом Жордана-Гаусса.

Найти : два общих и два соответствующих базисных решения

Решение :

Вычисления приведены в нижеследующей таблице:

Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель.

В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать.

Системы линейных уравнений. Лекция 6.

Системы линейных уравнений.

Основные понятия.

Система видa

называется системой - линейных уравнений с неизвестными .

Числа , , называются коэффициентами системы .

Числа , называются свободными членами системы , – переменными системы . Матрица

называется основной матрицей системы , а матрица

– расширенной матрицей системы . Матрицы - столбцы

И - соответственно матрицами свободных членов и неизвестных системы . Тогда в матричной форме систему уравнений можно записать в виде . Решением системы называется значений переменных , при подстановке которых, все уравнения системы обращаются в верные числовые равенства. Всякое решение системы можно представить в виде матрицы - столбца . Тогда справедливо матричное равенство .

Система уравнений называется совместной если она имеет хотя бы одно решение и несовместной если не имеет ни одного решения.

Решить систему линейных уравнений это значит выяснить совместна ли она и в случае совместности найти её общее решение.

Система называется однородной если все её свободные члены равны нулю. Однородная система всегда совместна, так как имеет решение

Теорема Кронекера – Копелли.

Ответ на вопрос существования решений линейных систем и их единственности позволяет получить следующий результат, который можно сформулировать в виде следующих утверждений относительно системы линейных уравнений с неизвестными

(1)

Теорема 2 . Система линейных уравнений (1) совместна тогда и только тогда когда ранг основной матрицы равен рангу расширенной (.

Теорема 3 . Если ранг основной матрицы совместной системы линейных уравнений равен числу неизвестных, то система имеет единственное решение.

Теорема 4 . Если ранг основной матрицы совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.

Правила решения систем.

3. Находят выражение главных переменных через свободные и получают общее решение системы.

4. Придавая свободным переменным произвольные значения получают все значения главных переменных.

Методы решения систем линейных уравнений.

Метод обратной матрицы.

причем , т. е. система имеет единственное решение. Запишем систему в матричном виде

где , , .

Умножим обе части матричного уравнения слева на матрицу

Так как , то получаем , откуда получаем равенство для нахождения неизвестных

Пример 27. Методом обратной матрицы решить систему линейных уравнений

Решение. Обозначим через основную матрицу системы

Пусть , тогда решение найдем по формуле .

Вычислим .

Так как , то и система имеет единственное решение. Найдем все алгебраические дополнения

, ,

Таким образом

Сделаем проверку

Обратная матрица найдена верно. Отсюда по формуле , найдем матрицу переменных .

Сравнивая значения матриц, получим ответ: .

Метод Крамера.

Пусть дана система линейных уравнений с неизвестными

причем , т. е. система имеет единственное решение. Запишем решение системы в матричном виде или

Обозначим

. . . . . . . . . . . . . . ,

Таким образом, получаем формулы для нахождения значений неизвестных, которые называются формулами Крамера .

Пример 28. Решить методом Крамера следующую систему линейных уравнений .

Решение. Найдем определитель основной матрицы системы

Так как , то , система имеет единственное решение.

Найдем остальные определители для формул Крамера

По формулам Крамера находим значения переменных

Метод Гаусса.

Метод заключается в последовательном исключении переменных.

Пусть дана система линейных уравнений с неизвестными.

Процесс решения по методу Гаусса состоит из двух этапов:

На первом этапе расширенная матрица системы приводится с помощью элементарных преобразований к ступенчатому виду

где , которой соответствует система

После этого переменные считаются свободными и в каждом уравнении переносятся в правую часть.

На втором этапе из последнего уравнения выражается переменная , полученное значение подставляется в уравнение. Из этого уравнения

выражается переменная . Этот процесс продолжается до первого уравнения. В результате получается выражение главных переменных через свободные переменные .

Пример 29. Решить методом Гаусса следующую систему

Решение. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду

Так как больше числа неизвестных, то система совместна и имеет бесконечное множество решений. Запишем систему для ступенчатой матрицы

Определитель расширенной матрицы этой системы, составленный из трех первых столбцов не равен нулю, поэтому его считаем базисным. Переменные

Будут базисными а переменная – свободной. Перенесем ее во всех уравнениях в левую часть

Из последнего уравнения выражаем

Подставив это значение в предпоследнее второе уравнение, получим

откуда . Подставив значения переменных и в первое уравнение, найдем . Ответ запишем в следующем виде

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

На основании теоремы Крамера

………….
,

где
-

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором, решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы - (2; -1; 1).

6. Общая система линейных алгебраических уравнений. Метод Гаусса.

Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений , который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной ).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья . Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы :
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка : рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .

На практике так подробно, конечно, не расписывают, а пишут короче:

Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку: »

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ : рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!

Вернемся к нашей системе . Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :

(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .

В нижнем уравнении у нас уже готовый результат: .

Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:

И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:

Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения . Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО :

А мысленный ход самих расчётов я уже рассмотрел выше.

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:

Круто.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:

Ответ :

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Пример 2

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!

Пример 3

Решить систему линейных уравнений методом Гаусса

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:

Ответ : .

Пример 4

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.

В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:

Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:

Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .

Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.

Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Дождливая осенняя погода за окном.... Поэтому для всех желающих более сложный пример для самостоятельного решения:

Пример 5

Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.

Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Желаю успехов!

Решения и ответы:

Пример 2: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход:

Ответ : .

Пример 4: Решение : Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы

(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
Нужная вещь на второй ступеньке получена .
(5) К третьей строке прибавили вторую, умноженную на 6.

В рамках уроков метод Гаусса и Несовместные системы/системы с общим решением мы рассматривали неоднородные системы линейных уравнений , где свободный член (который обычно находится справа) хотя бы одного из уравнений был отличен от нуля.
И сейчас, после хорошей разминки с рангом матрицы , мы продолжим шлифовать технику элементарных преобразований на однородной системе линейных уравнений .
По первым абзацам материал может показаться скучным и заурядным, однако данное впечатление обманчиво. Помимо дальнейшей отработки технических приёмов будет много новой информации, поэтому, пожалуйста, постарайтесь не пренебрегать примерами данной статьи.