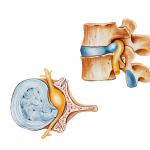
სიბრტყე ფიგურაზე წერტილების სიჩქარის განსაზღვრა მყისიერი სიჩქარის ცენტრის გამოყენებით. ბრტყელი ფიგურის წერტილების სიჩქარის განსაზღვრა სიბრტყეზე მოძრაობისას ფიგურის წერტილის სიჩქარის განსაზღვრა
ლექცია 3. ხისტი სხეულის სიბრტყე-პარალელური მოძრაობა. სიჩქარისა და აჩქარების განსაზღვრა.
ეს ლექცია მოიცავს შემდეგ საკითხებს:
1. ხისტი სხეულის სიბრტყე-პარალელური მოძრაობა.
2. სიბრტყე-პარალელური მოძრაობის განტოლებები.
3. მოძრაობის დაშლა მთარგმნელობით და ბრუნვით.
4. წერტილოვანი სიჩქარის განსაზღვრა ბრტყელი ფიგურა.
5. თეორემა სხეულის ორი წერტილის სიჩქარის პროგნოზების შესახებ.
6. სიბრტყე ფიგურის წერტილების სიჩქარის განსაზღვრა სიჩქარის მყისიერი ცენტრის გამოყენებით.
7. ამოცანების გადაჭრა სიჩქარის განსაზღვრაზე.
8. სიჩქარის გეგმა.
9. სიბრტყე ფიგურის წერტილების აჩქარებების განსაზღვრა.
10. აჩქარების ამოცანების ამოხსნა.
11. მყისიერი აჩქარების ცენტრი.
ამ საკითხების შესწავლა აუცილებელია მომავალში ხისტი სხეულის სიბრტყით მოძრაობის დინამიკის, ფარდობითი მოძრაობის დინამიკისათვის. მატერიალური წერტილი, ამოცანების გადაჭრა დისციპლინებში „მანქანებისა და მექანიზმების თეორია“ და „მანქანის ნაწილები“.
ხისტი სხეულის სიბრტყე-პარალელური მოძრაობა. სიბრტყე-პარალელური მოძრაობის განტოლებები.
მოძრაობის დაშლა მთარგმნელობით და ბრუნვად
ხისტი სხეულის სიბრტყე-პარალელური (ან ბრტყელი) მოძრაობა ეწოდება ისე, რომ მისი ყველა წერტილი მოძრაობს რაიმე ფიქსირებული სიბრტყის პარალელურად. პ(სურ. 28). თვითმფრინავის მოძრაობას ახორციელებს მექანიზმებისა და მანქანების მრავალი ნაწილი, მაგალითად, მოძრავი ბორბალი ლიანდაგის სწორ მონაკვეთზე, შემაერთებელი ღერო ამწე-სლაიდერ მექანიზმში და ა.შ. სიბრტყე-პარალელური მოძრაობის განსაკუთრებული შემთხვევაა ბრუნვის მოძრაობა. ხისტი სხეულის ფიქსირებული ღერძის გარშემო.

სურ.28 სურ.29
განვიხილოთ განყოფილება სზოგიერთი თვითმფრინავის სხეულები ოქსი, თვითმფრინავის პარალელურად პ(სურ. 29). სიბრტყე-პარალელური მოძრაობისას სხეულის ყველა წერტილი სწორ ხაზზე დევს მმ“, დინების პერპენდიკულარულად ს, ანუ თვითმფრინავები პ, იმოძრავეთ იდენტურად.
აქედან ვასკვნით, რომ მთელი სხეულის მოძრაობის შესასწავლად საკმარისია იმის შესწავლა, თუ როგორ მოძრაობს იგი სიბრტყეში ოჰოოგანყოფილება სეს სხეული ან რომელიმე ბრტყელი ფიგურა ს. ამიტომ, მომავალში სხეულის სიბრტყეზე მოძრაობის ნაცვლად განვიხილავთ სიბრტყე ფიგურის მოძრაობას. სთავის სიბრტყეში, ე.ი. თვითმფრინავში ოჰოო.
ფიგურის პოზიცია სთვითმფრინავში ოჰოოგანისაზღვრება ამ ფიგურაზე დახატული ნებისმიერი სეგმენტის პოზიციით AB(სურ. 28). თავის მხრივ, სეგმენტის პოზიცია ABშეიძლება განისაზღვროს კოორდინატების ცოდნით xა და წა ქულა ადა კუთხე, რომელიც არის სეგმენტი ABაყალიბებს ღერძით X. სრული გაჩერება ა, შერჩეული ფიგურის პოზიციის დასადგენად ს, ჩვენ შემდგომ მას პოლუსს დავარქმევთ.
სიდიდის ფიგურის გადაადგილებისას xა და წა და შეიცვლება. იცოდე მოძრაობის კანონი, ანუ ფიგურის მდებარეობა სიბრტყეში ოჰოონებისმიერ დროს, თქვენ უნდა იცოდეთ დამოკიდებულებები
განტოლებებს, რომლებიც განსაზღვრავენ მიმდინარე მოძრაობის კანონს, ეწოდება ბრტყელი ფიგურის მოძრაობის განტოლებები მის სიბრტყეში. ისინი ასევე არის ხისტი სხეულის სიბრტყე-პარალელური მოძრაობის განტოლებები.
მოძრაობის განტოლებიდან პირველი ორი განსაზღვრავს მოძრაობას, რომელსაც ფიგურა გააკეთებს, თუ =const; ეს, ცხადია, იქნება მთარგმნელობითი მოძრაობა, რომელშიც ფიგურის ყველა წერტილი მოძრაობს ისევე, როგორც პოლუსი ა. მესამე განტოლება განსაზღვრავს მოძრაობას, რომელსაც ფიგურა გააკეთებს, თუ და, ე.ი. როცა ბოძი აუმოძრაო; ეს იქნება ფიგურის ბრუნვა ბოძის გარშემო ა. აქედან შეგვიძლია დავასკვნათ, რომ ზოგად შემთხვევაში ბრტყელი ფიგურის მოძრაობა მის სიბრტყეში შეიძლება ჩაითვალოს, როგორც მთარგმნელობითი მოძრაობისგან შემდგარი, რომელშიც ფიგურის ყველა წერტილი მოძრაობს ისევე, როგორც პოლუსი. ადა ამ პოლუსის გარშემო ბრუნვითი მოძრაობიდან.
განსახილველი მოძრაობის ძირითადი კინემატიკური მახასიათებლებია მთარგმნელობითი მოძრაობის სიჩქარე და აჩქარება, ტოლი პოლუსის სიჩქარისა და აჩქარების, აგრეთვე ბოძის გარშემო ბრუნვის მოძრაობის კუთხური სიჩქარე და კუთხური აჩქარება.
სიბრტყე ფიგურაზე წერტილების სიჩქარის განსაზღვრა
აღინიშნა, რომ ბრტყელი ფიგურის მოძრაობა შეიძლება ჩაითვალოს, როგორც მთარგმნელობითი მოძრაობისგან შემდგარი, რომელშიც ფიგურის ყველა წერტილი მოძრაობს ბოძის სიჩქარით. ადა ამ პოლუსის გარშემო ბრუნვითი მოძრაობიდან. ვაჩვენოთ, რომ ნებისმიერი წერტილის სიჩქარე მფიგურა გეომეტრიულად შედგება იმ სიჩქარისგან, რომელსაც წერტილი იღებს თითოეულ ამ მოძრაობაში.
სინამდვილეში, ნებისმიერი წერტილის პოზიცია მფიგურები განისაზღვრება ცულებთან მიმართებაში ოჰოორადიუსის ვექტორი (სურ. 30), სადაც არის ბოძის რადიუსის ვექტორი ა, - წერტილის პოზიციის განმსაზღვრელი ვექტორი მბოძთან მოძრავ ღერძებთან შედარებით ამთარგმნელობითად (ფიგურის მოძრაობა ამ ღერძებთან მიმართებაში არის ბრუნვა ბოძის გარშემო ა). მერე
![]()
![]()
![]()
5) წინსვლა.მაგალითები.
სხეულის ბრუნვის მოძრაობის განსაზღვრა ფიქსირებული ღერძის გარშემო.
ბრუნვის მოძრაობის განტოლება.
- მოძრაობა, რომლის დროსაც მისი ყველა წერტილი მოძრაობს სიბრტყეზე პერპენდიკულარულად რაიმე ფიქსირებული ხაზის მიმართ და აღწერს წრეებს ამ წრფეზე მდებარე ცენტრებით, რომელსაც ბრუნვის ღერძი ეწოდება.
მოძრაობა მოცემულია ფ (ბრუნვის კუთხე) დიედრული კუთხის ცვლილების კანონით, რომელიც წარმოიქმნება ბრუნვის ღერძზე გამავალი ფიქსირებული P სიბრტყით და სხეულთან მყარად დაკავშირებული სიბრტყე Q:
კუთხური სიჩქარე არის სიდიდე, რომელიც ახასიათებს ბრუნვის კუთხის ცვლილების სიჩქარეს.
კუთხური აჩქარება არის სიდიდე, რომელიც ახასიათებს კუთხური სიჩქარის ცვლილების სიჩქარეს.
ბრტყელ ფიგურაზე ნებისმიერი წერტილის სიჩქარის განსაზღვრა.
სიჩქარის დასადგენად 1 გზა არის ვექტორების მეშვეობით. ბრტყელ ფიგურაზე ნებისმიერი წერტილის სიჩქარე უდრის ბოძის სიჩქარის გეომეტრიულ ჯამს და ამ წერტილის ბრუნვის სიჩქარეს ბოძის გარშემო. ამრიგად, B წერტილის სიჩქარე ტოლია A პოლუსის სიჩქარისა და B წერტილის ბრუნვის სიჩქარის გეომეტრიული ჯამის პოლუსის გარშემო:
სიჩქარის განსაზღვრის მე-2 გზა - პროგნოზების საშუალებით. (სიჩქარის პროექციის თეორემა) სიბრტყის წერტილების სიჩქარის პროგნოზები ამ წერტილებზე გამავალ ღერძზე ტოლია.
3) წერტილის სიჩქარისა და აჩქარების გამოსათვლელი ფორმულები მისი მოძრაობის დაზუსტების ბუნებრივი გზით.
სიჩქარის ვექტორი; - სიჩქარის პროექცია ტანგენტზე;
აჩქარების ვექტორის კომპონენტები; ![]() -აჩქარების პროგნოზები t და n ღერძებზე;
-აჩქარების პროგნოზები t და n ღერძებზე;
ამრიგად, წერტილის მთლიანი აჩქარება არის ორი აჩქარების ვექტორული ჯამი:
ტანგენტი მიმართული ტანგენსი ტრაექტორიაზე რკალის კოორდინატის გაზრდის მიმართულებით, თუ (ში წინააღმდეგ შემთხვევაში- საპირისპირო მიმართულებით) და
ნორმალური აჩქარება მიმართული ნორმალურის გასწვრივ ტანგენტისკენ გამრუდების ცენტრისკენ (ტრაექტორიის ჩაზნექილი): აჩქარების მთლიანი მოდული: ![]()
4) წერტილის სიჩქარისა და აჩქარების გამოსათვლელი ფორმულები დეკარტის კოორდინატებში მისი მოძრაობის დაზუსტების კოორდინატული მეთოდის გამოყენებით.
სიჩქარის ვექტორის კომპონენტები: -სიჩქარის პროგნოზები კოორდინატთა ღერძებზე:
![]() - აჩქარების ვექტორის კომპონენტები; -აჩქარების პროგნოზები კოორდინატთა ღერძზე;
- აჩქარების ვექტორის კომპონენტები; -აჩქარების პროგნოზები კოორდინატთა ღერძზე;
5) წინსვლა.მაგალითები.
(სლაიდერი, ტუმბოს დგუში, ორთქლის ლოკომოტივის წყვილი ბორბალი, რომელიც მოძრაობს სწორ გზაზე, ლიფტის სალონი, კუპეს კარი, ეშმაკის ბორბალი - ეს არის მოძრაობა, რომლის დროსაც ნებისმიერი სწორი ხაზი, რომელიც მკაცრად არის დაკავშირებული სხეულთან, რჩება თავის პარალელურად). ჩვეულებრივ, მთარგმნელობითი მოძრაობა იდენტიფიცირებულია მისი წერტილების სწორხაზოვანი მოძრაობით, მაგრამ ეს ასე არ არის. წერტილებს და თავად სხეულს (სხეულის მასის ცენტრს) შეუძლიათ გადაადგილება მოხრილი ტრაექტორიების გასწვრივ, იხილეთ, მაგალითად, ეშმაკის ბორბლის სალონის მოძრაობა. სხვა სიტყვებით რომ ვთქვათ, ეს არის მოძრაობა მონაცვლეობის გარეშე.
სიბრტყე ფიგურაზე წერტილების სიჩქარის განსაზღვრა
აღინიშნა, რომ ბრტყელი ფიგურის მოძრაობა შეიძლება ჩაითვალოს მთარგმნელობითი მოძრაობისგან, რომელშიც ფიგურის ყველა წერტილი მოძრაობს სიჩქარით.ბოძები ადა ამ პოლუსის გარშემო ბრუნვითი მოძრაობიდან. ვაჩვენოთ, რომ ნებისმიერი წერტილის სიჩქარე მფიგურა გეომეტრიულად იქმნება სიჩქარისგან, რომელსაც წერტილი იღებს თითოეულ ამ მოძრაობაში.
სინამდვილეში, ნებისმიერი წერტილის პოზიცია მფიგურები განისაზღვრება ცულებთან მიმართებაში ოჰოორადიუსის ვექტორი(სურ. 3), სადაც - ბოძის რადიუსის ვექტორი ა , - წერტილის პოზიციის განმსაზღვრელი ვექტორი მცულებთან შედარებით, ბოძთან ერთად მოძრავი ამთარგმნელობითად (ფიგურის მოძრაობა ამ ღერძებთან მიმართებაში არის ბრუნვა ბოძის გარშემო ა). მერე
![]()
მიღებულ თანასწორობაში რაოდენობაარის ბოძის სიჩქარე ა; იგივე ზომასიჩქარის ტოლი , რომელი წერტილი მიღებს ზე, ე.ი. ცულებთან შედარებით, ან, სხვა სიტყვებით რომ ვთქვათ, როდესაც ფიგურა ბრუნავს ბოძის გარშემო ა. ამდენად, წინა თანასწორობიდან ეს ნამდვილად გამომდინარეობს
სიჩქარე , რომელი წერტილი მმიღებული ბოძის გარშემო ფიგურის ბრუნვით ა :
სადაც ω - ფიგურის კუთხური სიჩქარე.
ამრიგად, ნებისმიერი წერტილის სიჩქარე მბრტყელი ფიგურა გეომეტრიულად არის სხვა წერტილის სიჩქარის ჯამი ა, მიღებული როგორც პოლუსი და სიჩქარე, რომელიც წერტილი მმიღებული ფიგურის ამ ბოძის გარშემო ბრუნვით. მოდული და სიჩქარის მიმართულებაგვხვდება შესაბამისი პარალელოგრამის აგებით (სურ. 4).


სურ.3ნახ.4
თეორემა სხეულზე ორი წერტილის სიჩქარის პროგნოზების შესახებ
სიბრტყე ფიგურის (ან სხეულის პარალელურად მოძრავი სიბრტყეზე) წერტილების სიჩქარის განსაზღვრა ჩვეულებრივ მოიცავს საკმაოდ რთულ გამოთვლებს. თუმცა, შესაძლებელია ფიგურის (ან სხეულის) წერტილების სიჩქარის დასადგენად მრავალი სხვა, პრაქტიკულად უფრო მოსახერხებელი და მარტივი მეთოდის მიღება.

ნახ.5
ერთ-ერთი ასეთი მეთოდი მოცემულია თეორემით: ხისტი სხეულის ორი წერტილის სიჩქარის პროგნოზები ამ წერტილებზე გამავალ ღერძზე ერთმანეთის ტოლია. განვიხილოთ ორი პუნქტი ადა INბრტყელი ფიგურა (ან სხეული). პუნქტის აღება აბოძზე (ნახ. 5), ვიღებთ. აქედან გამომდინარე, ტოლობის ორივე მხარის პროექცია გასწვრივ მიმართულ ღერძზე ABდა იმის გათვალისწინებით, რომ ვექტორიპერპენდიკულარული AB, ვპოულობთ
და თეორემა დადასტურებულია.
სიბრტყე ფიგურაზე წერტილების სიჩქარის განსაზღვრა მყისიერი სიჩქარის ცენტრის გამოყენებით.
ბრტყელი ფიგურის (ან სხეულის სიბრტყეზე მყოფი სხეულის) წერტილების სიჩქარის განსაზღვრის კიდევ ერთი მარტივი და ვიზუალური მეთოდი ეფუძნება სიჩქარის მყისიერი ცენტრის კონცეფციას.
მყისიერი სიჩქარის ცენტრი არის ბრტყელი ფიგურის წერტილი, რომლის სიჩქარე დროის მოცემულ მომენტში არის ნული.
ამის გადამოწმება ადვილია, თუ ფიგურა მოძრაობს არაპროგრესულად, მაშინ ასეთი წერტილი დროის ყოველ მომენტში ტარსებობს და უფრო მეტიც, ერთადერთია. ნება მომენტში ტქულები ადა INბრტყელ ფიგურებს აქვთ სიჩქარედა , არა ერთმანეთის პარალელურად (სურ. 6). შემდეგ მიუთითეთ რ, წევს პერპენდიკულარების გადაკვეთაზე აჰვექტორამდედა IN ბვექტორამდე და მას შემდეგ იქნება მყისიერი სიჩქარის ცენტრი. მართლაც, თუ ვივარაუდებთ, რომ, შემდეგ სიჩქარის პროექციის თეორემით ვექტორიუნდა იყოს პერპენდიკულარულიც და AR(რადგან) და VR(რადგან), რაც შეუძლებელია. ამავე თეორემიდან ირკვევა, რომ ფიგურის არცერთ სხვა წერტილს დროის ამ მომენტში არ შეიძლება ჰქონდეს ნულის ტოლი სიჩქარე.

სურ.6
თუ ახლა დროის მომენტში ავიღებთ პუნქტს რბოძის უკან, შემდეგ წერტილის სიჩქარე ანება
რადგან . ანალოგიური შედეგი მიიღება ფიგურის ნებისმიერი სხვა წერტილისთვის. შესაბამისად, სიბრტყე ფიგურის წერტილების სიჩქარე განისაზღვრება მომენტშიდრო თითქოს ფიგურის მოძრაობა იყოს ბრუნვა სიჩქარის მყისიერი ცენტრის გარშემო. ამავე დროს
თანასწორობიდან ისიც გამომდინარეობს, რომბრტყელი ფიგურის წერტილები პროპორციულია MCS-დან მათი დაშორების.
მიღებული შედეგები იწვევს შემდეგ დასკვნებს.
1. სიჩქარის მყისიერი ცენტრის დასადგენად, თქვენ მხოლოდ უნდა იცოდეთ სიჩქარის მიმართულებებიდა ორი წერტილი ადა INბრტყელი ფიგურა (ან ამ წერტილების ტრაექტორია); სიჩქარის მყისიერი ცენტრი მდებარეობს წერტილებიდან აგებული პერპენდიკულარების გადაკვეთის ადგილზე. ადა INამ წერტილების სიჩქარეებზე (ან ტრაექტორიების ტანგენტებზე).
2. ბრტყელ ფიგურაზე ნებისმიერი წერტილის სიჩქარის დასადგენად, თქვენ უნდა იცოდეთ რომელიმე წერტილის სიჩქარის სიდიდე და მიმართულება. აფიგურა და მისი სხვა წერტილის სიჩქარის მიმართულება IN. შემდეგ, ქულების აღდგენა ადა INპერპენდიკულარულიდა , ავაშენოთ მყისიერი სიჩქარის ცენტრი რდა მიმართულებითგანვსაზღვროთ ფიგურის ბრუნვის მიმართულება. ამის შემდეგ იცის, მოდი ვიპოვოთ სიჩქარენებისმიერი წერტილი მბრტყელი ფიგურა. მიმართული ვექტორიპერპენდიკულარული RMფიგურის ბრუნვის მიმართულებით.
3. კუთხური სიჩქარებრტყელი ფიგურა დროის თითოეულ მოცემულ მომენტში უდრის ფიგურის ნებისმიერი წერტილის სიჩქარის თანაფარდობას სიჩქარის მყისიერი ცენტრიდან მის დაშორებას რ :
განვიხილოთ მყისიერი სიჩქარის ცენტრის განსაზღვრის რამდენიმე განსაკუთრებული შემთხვევა.
ა) თუ სიბრტყე-პარალელური მოძრაობა ხორციელდება ერთი ცილინდრული სხეულის სხვა სტაციონარული სხეულის ზედაპირის გასწვრივ სრიალის გარეშე, მაშინ წერტილი რ მოძრავი სხეულის, რომელიც ეხება უძრავ ზედაპირს (ნახ. 7), დროის მოცემულ მომენტში, სრიალის არარსებობის გამო, აქვს ნულის ტოლი სიჩქარე (), და, შესაბამისად, არის სიჩქარის მყისიერი ცენტრი. ამის მაგალითია ბორბალი, რომელიც მოძრავია ლიანდაგზე.
ბ) თუ წერტილების სიჩქარეები ადა INბრტყელი ფიგურები ერთმანეთის პარალელურია და ხაზი ABარა პერპენდიკულარული(ნახ. 8, ა), მაშინ სიჩქარის მყისიერი ცენტრი დევს უსასრულობაში და ყველა წერტილის სიჩქარე პარალელურია. უფრო მეტიც, სიჩქარის პროგნოზების თეორემიდან გამომდინარეობს, რომე.ი. ; მსგავსი შედეგი მიიღება ყველა სხვა პუნქტისთვის. შესაბამისად, განსახილველ შემთხვევაში, ფიგურის ყველა წერტილის სიჩქარე დროის მოცემულ მომენტში ტოლია ერთმანეთის სიდიდითაც და მიმართულებითაც, ე.ი. ფიგურას აქვს სიჩქარის მყისიერი მთარგმნელობითი განაწილება (სხეულის მოძრაობის ამ მდგომარეობას ასევე უწოდებენ მყისიერ ტრანსლაციას). კუთხური სიჩქარესხეული დროის ამ მომენტში, როგორც ჩანს, ნულის ტოლია.

ნახ.7

სურ.8
გ) თუ წერტილების სიჩქარეები ადა INბრტყელი ფიგურები ერთმანეთის პარალელურია და ამავდროულად ხაზიც ABპერპენდიკულარული, შემდეგ მყისიერი სიჩქარის ცენტრი რგანისაზღვრება 8-ზე ნაჩვენები კონსტრუქციით, ბ. კონსტრუქციების სამართლიანობა პროპორციიდან გამომდინარეობს. ამ შემთხვევაში, წინაგან განსხვავებით, ცენტრის პოვნა რმიმართულებების გარდა, თქვენ ასევე უნდა იცოდეთ სიჩქარის მოდულები.
დ) თუ ცნობილია სიჩქარის ვექტორირაღაც წერტილი INფიგურა და მისი კუთხური სიჩქარე, შემდეგ მყისიერი სიჩქარის ცენტრის პოზიცია რ, წევს პერპენდიკულარულად(სურ. 8, ბ), გვხვდება როგორც.
სიჩქარის განსაზღვრის პრობლემების გადაჭრა.
საჭირო კინემატიკური მახასიათებლების (სხეულის კუთხური სიჩქარე ან მისი წერტილების სიჩქარე) დასადგენად, საჭიროა ვიცოდეთ რომელიმე წერტილის სიჩქარის სიდიდე და მიმართულება და სხვა განივი წერტილის სიჩქარის მიმართულება. ამ ორგანოს. გადაწყვეტა უნდა დაიწყოს ამ მახასიათებლების განსაზღვრით პრობლემის მონაცემებზე დაყრდნობით.
მექანიზმი, რომლის მოძრაობაც შესწავლილია, ნახატზე უნდა იყოს გამოსახული იმ პოზიციაზე, რისთვისაც აუცილებელია შესაბამისი მახასიათებლების დადგენა. გაანგარიშებისას უნდა გვახსოვდეს, რომ მყისიერი სიჩქარის ცენტრის კონცეფცია ვრცელდება მოცემულ ხისტ სხეულზე. მექანიზმში, რომელიც შედგება რამდენიმე სხეულისგან, თითოეულ არამთარგმნელობით მოძრავ სხეულს აქვს თავისი მყისიერი სიჩქარის ცენტრი დროის მოცემულ მომენტში. რდა მისი კუთხური სიჩქარე.
მაგალითი 1.კოჭის ფორმის სხეული თავისი შუა ცილინდრით სტაციონარული სიბრტყის გასწვრივ ისე მოძრაობს(სმ). ცილინდრის რადიუსი:რ= 4 მედია რ= 2 სმ (ნახ. 9). .

ნახ.9
გამოსავალი.მოდით განვსაზღვროთ წერტილების სიჩქარე A, Bდა თან.
სიჩქარის მყისიერი ცენტრი მდებარეობს ხვეულის თვითმფრინავთან შეხების წერტილში.
SpeedPole თან .
|
|
![]()
წერტილის სიჩქარე ადა INმიმართულია პერპენდიკულურად იმ სწორ სეგმენტებზე, რომლებიც აკავშირებენ ამ წერტილებს სიჩქარის მყისიერ ცენტრთან. სიჩქარეები:
მაგალითი 2.რადიუსის ბორბალი რ= 0,6 მ რულონები ბილიკის სწორი მონაკვეთის გასწვრივ სრიალის გარეშე (ნახ. 9.1); მისი C ცენტრის სიჩქარე მუდმივი და ტოლიავ გ
= 12 მ/წმ. იპოვნეთ ბორბლის კუთხოვანი სიჩქარე და ბოლოების სიჩქარე მ 1 , მ 2 , მ 3 , მ 4 ვერტიკალური და ჰორიზონტალური ბორბლის დიამეტრი.
სურ.9.1
გამოსავალი. ბორბალი ასრულებს სიბრტყე პარალელურ მოძრაობას. ბორბლის სიჩქარის მყისიერი ცენტრი მდებარეობს ჰორიზონტალურ სიბრტყესთან შეხების M1 წერტილში, ე.ი.
ბორბლის კუთხოვანი სიჩქარე
![]()
იპოვეთ M2, M3 და M4 წერტილების სიჩქარეები
მაგალითი3 . რადიუსის მანქანის ამძრავი ბორბალი რ= 0,5 მ რულონები მოცურებით (სრიალებით) მაგისტრალის სწორი მონაკვეთის გასწვრივ; მისი ცენტრის სიჩქარე თანარის მუდმივი და თანაბარივ გ
= 4 მ/წმ. ბორბლის სიჩქარის მყისიერი ცენტრი არის წერტილში რმანძილზე თ = მოძრავი თვითმფრინავიდან 0,3 მ. იპოვეთ ბორბლის კუთხური სიჩქარე და წერტილების სიჩქარე ადა INმისი ვერტიკალური დიამეტრი.
სურ.9.2
გამოსავალი.ბორბლის კუთხოვანი სიჩქარე
ქულების სიჩქარის პოვნა ადა IN
მაგალითი 4.იპოვეთ შემაერთებელი ღეროს კუთხური სიჩქარე ABდა ქულების სიჩქარე IN და ამწე მექანიზმის C (ნახ. 9.3, ა). მოცემულია ამწის კუთხოვანი სიჩქარე ო.ა.და ზომები: ω OA = 2 ს -1, ო.ა. =AB = 0.36 მ, AC= 0,18 მ.
ა)
 ბ)
ბ)

სურ.9.3
გამოსავალი.კრაკი ო.ა.აკეთებს ბრუნვის მოძრაობას, შემაერთებელ ღეროს AB- სიბრტყე-პარალელური მოძრაობა (ნახ. 9.3, ბ).
წერტილის სიჩქარის პოვნა აბმული
ო.ა.
წერტილის სიჩქარე INმიმართულია ჰორიზონტალურად. წერტილების სიჩქარის მიმართულების ცოდნა ადა INდამაკავშირებელი ღერო AB,განსაზღვრეთ მისი მყისიერი სიჩქარის ცენტრის პოზიცია - წერტილი R AV.
დააკავშირეთ კუთხური სიჩქარე ABდა ქულების სიჩქარე INდა C:
![]()
მაგალითი 5.ბირთვი ABსრიალებს მის ბოლოებს ორმხრივი პერპენდიკულარული სწორი ხაზების გასწვრივ ისე, რომ კუთხითსიჩქარე (ნახ. 10). ღეროს სიგრძე AB = ლ. განვსაზღვროთ დასასრულის სიჩქარე ადა ღეროს კუთხური სიჩქარე.

სურ.10
გამოსავალი.ძნელი არ არის წერტილის სიჩქარის ვექტორის მიმართულების დადგენა ავერტიკალური სწორი ხაზის გასწვრივ სრიალი. მერეარის პერპენდიკულარების გადაკვეთაზედა (სურ. 10).
კუთხური სიჩქარე
![]()
წერტილის სიჩქარე ა :
|
|
![]()
სიჩქარის გეგმა.
მოდით, სხეულის ბრტყელი მონაკვეთის რამდენიმე წერტილის სიჩქარე იყოს ცნობილი (სურ. 11). თუ ეს სიჩქარეები გამოსახულია სკალაზე გარკვეული წერტილიდან შესახებდა დააკავშირეთ მათი ბოლოები სწორი ხაზებით, მიიღებთ სურათს, რომელსაც სიჩქარის გეგმა ჰქვია. (სურათზე) .

სურ.11
სიჩქარის გეგმის თვისებები.
|
|
მართლა, . მაგრამ სიჩქარის თვალსაზრისით![]() . ნიშნავსდა პერპენდიკულარული ABმაშასადამე.ზუსტად იგივე.
. ნიშნავსდა პერპენდიკულარული ABმაშასადამე.ზუსტად იგივე.
ბ) სიჩქარის გეგმის გვერდები სხეულის სიბრტყეზე შესაბამისი სწორი მონაკვეთების პროპორციულია.
იმიტომ რომ
, მაშინ აქედან გამომდინარეობს, რომ სიჩქარის გეგმის გვერდები სხეულის სიბრტყეზე სწორი სეგმენტების პროპორციულია.ამ თვისებების კომბინაციით შეგვიძლია დავასკვნათ, რომ სიჩქარის გეგმა მსგავსია სხეულის შესაბამისი ფიგურისა და ბრუნავს მასზე 90˚ ბრუნვის მიმართულებით სიჩქარის გეგმის ეს თვისებები საშუალებას გაძლევთ განსაზღვროთ სხეულის წერტილების სიჩქარე.
მაგალითი 6.სურათი 12 გვიჩვენებს მასშტაბის მექანიზმს. ცნობილი კუთხური სიჩქარებმული OA.

სურ.12
გამოსავალი.სიჩქარის გეგმის ასაგებად, ერთი წერტილის სიჩქარე და მეორის სიჩქარის ვექტორის მიმართულება მაინც უნდა იყოს ცნობილი. ჩვენს მაგალითში შეგვიძლია განვსაზღვროთ წერტილის სიჩქარე ა : და მისი ვექტორის მიმართულება.

სურ.13
|
|
სიჩქარის წერტილები ეუდრის ნულს, ამიტომ წერტილი ესიჩქარის გეგმაზე ემთხვევა პუნქტს შესახებ.
შემდეგი უნდა იყოს
და . ჩვენ ვხატავთ ამ ხაზებს და ვპოულობთ მათ გადაკვეთის წერტილსდ.სეგმენტი ო დ დაადგენს სიჩქარის ვექტორს.მაგალითი 7.არტიკულირებულში ოთხი ბმულიOABCამძრავი ამწეო.ა.სმ ერთნაირად ბრუნავს ღერძის გარშემო შესახებკუთხური სიჩქარითω = 4 s -1 და დამაკავშირებელი ღეროს გამოყენებით AB= 20 სმ იწვევს ამწის ბრუნვას მზეღერძის გარშემო თან(ნახ. 13.1, ა). განსაზღვრეთ ქულების სიჩქარე ადა IN,ასევე შემაერთებელი ღეროს კუთხური სიჩქარეები ABდა ამწე მზე.
ა)
 ბ)
ბ)

სურ.13.1
გამოსავალი.წერტილის სიჩქარე აამწე ო.ა.
პუნქტის აღება აბოძის უკან შევქმნათ ვექტორული განტოლება
სად
ამ განტოლების გრაფიკული ამოხსნა მოცემულია ნახ. 13.1-ში ,ბ(სიჩქარის გეგმა).
სიჩქარის გეგმის გამოყენებით მივიღებთ
![]()
შემაერთებელი ღეროს კუთხური სიჩქარე AB
![]()
წერტილის სიჩქარე IN შეიძლება მოიძებნოს თეორემის გამოყენებით სხეულის ორი წერტილის სიჩქარის პროგნოზების შესახებ მათ დამაკავშირებელ სწორ ხაზზე.
B და ამწეის კუთხური სიჩქარე NE
![]()
სიბრტყე ფიგურის წერტილების აჩქარების განსაზღვრა
ვაჩვენოთ, რომ ნებისმიერი წერტილის აჩქარება მბრტყელი ფიგურის (ისევე როგორც სიჩქარის) შედგება აჩქარებისაგან, რომელსაც წერტილი იღებს ამ ფიგურის გადამყვანი და ბრუნვითი მოძრაობების დროს. წერტილის პოზიცია მცულებთან მიმართებაში შესახებ xy (იხ. სურ. 30) განისაზღვრება რადიუსის ვექტორი- კუთხე ვექტორს შორისდა სეგმენტი MA(სურ. 14).
ამრიგად, ნებისმიერი წერტილის აჩქარება მბრტყელი ფიგურა გეომეტრიულად შედგება სხვა წერტილის აჩქარებისგან აპოლუსად აღებული და აჩქარება, რომელიც არის წერტილი მმიღებული ფიგურის ამ ბოძის გარშემო ბრუნვით. აჩქარების მოდული და მიმართულება, გვხვდება შესაბამისი პარალელოგრამის აგებით (სურ. 23).
თუმცა, გაანგარიშება და აჩქარება რაღაც წერტილი აეს მაჩვენებელი ამ მომენტში; 2) სხვა წერტილის ტრაექტორია INფიგურები. ზოგიერთ შემთხვევაში, ფიგურის მეორე წერტილის ტრაექტორიის ნაცვლად, საკმარისია ვიცოდეთ სიჩქარის მყისიერი ცენტრის პოზიცია.
პრობლემების გადაჭრისას სხეული (ან მექანიზმი) უნდა იყოს გამოსახული იმ მდგომარეობაში, რისთვისაც აუცილებელია შესაბამისი წერტილის აჩქარების დადგენა. გამოთვლა იწყება პრობლემური მონაცემების საფუძველზე პოლუსად აღებული წერტილის სიჩქარის და აჩქარების დადგენით.
ამოხსნის გეგმა (თუ მოცემულია ბრტყელი ფიგურის ერთი წერტილის სიჩქარე და აჩქარება და ფიგურის სხვა წერტილის სიჩქარისა და აჩქარების მიმართულება):
1) იპოვეთ სიჩქარის მყისიერი ცენტრი ბრტყელი ფიგურის ორი წერტილის სიჩქარის პერპენდიკულარების აგებით.
2) განსაზღვრეთ ფიგურის მყისიერი კუთხური სიჩქარე.
3) ჩვენ განვსაზღვრავთ წერტილის ცენტრიდანულ აჩქარებას პოლუსის ირგვლივ, ნულის ტოლფასია აჩქარების ყველა ნაწილის პროგნოზების ჯამს აჩქარების ცნობილი მიმართულების პერპენდიკულარულ ღერძზე.
4) იპოვნეთ ბრუნვის აჩქარების მოდული ნულის ტოლფასით აჩქარების ყველა პუნქტის პროგნოზების ჯამის აჩქარების ცნობილი მიმართულების პერპენდიკულარულ ღერძზე.
5) აღმოჩენილი ბრუნვის აჩქარებიდან დაადგინეთ ბრტყელი ფიგურის მყისიერი კუთხოვანი აჩქარება.
6) იპოვეთ წერტილის აჩქარება ბრტყელ ფიგურაზე აჩქარების განაწილების ფორმულის გამოყენებით.
ამოცანების გადაჭრისას შეგიძლიათ გამოიყენოთ „თეორემა აბსოლუტურად ხისტი სხეულის ორი წერტილის აჩქარების ვექტორების პროგნოზებზე“:
”აბსოლუტურად ხისტი სხეულის ორი წერტილის აჩქარების ვექტორების პროგნოზები, რომლებიც ასრულებენ სიბრტყე პარალელურ მოძრაობას სწორ ხაზზე, ბრუნავს ამ ორ წერტილში გამავალ სწორ ხაზთან მიმართებაში, ამ სხეულის მოძრაობის სიბრტყეში კუთხით.კუთხური აჩქარების მიმართულებით ტოლია“.
ეს თეორემა მოსახერხებელია გამოსაყენებლად, თუ ცნობილია აბსოლუტურად ხისტი სხეულის მხოლოდ ორი წერტილის აჩქარება, როგორც სიდიდით, ასევე მიმართულებით, ცნობილია მხოლოდ ამ სხეულის სხვა წერტილების აჩქარების ვექტორების მიმართულებები (სხეულის გეომეტრიული ზომები არ არის ცნობილი), არ არის ცნობილიდა - შესაბამისად, ამ სხეულის კუთხური სიჩქარისა და კუთხური აჩქარების ვექტორების პროგნოზები მოძრაობის სიბრტყის პერპენდიკულარულ ღერძზე, ამ სხეულის წერტილების სიჩქარე ცნობილი არ არის.
ბრტყელი ფიგურის წერტილების აჩქარების დასადგენად კიდევ 3 ცნობილი გზა არსებობს:
1) მეთოდი ეფუძნება აბსოლუტურად ხისტი სხეულის სიბრტყე-პარალელური მოძრაობის კანონების ორჯერ დიფერენციაციას.
2) მეთოდი ეფუძნება აბსოლუტურად ხისტი სხეულის აჩქარების მყისიერი ცენტრის გამოყენებას (აბსოლუტურად ხისტი სხეულის აჩქარების მყისიერი ცენტრი ქვემოთ იქნება განხილული).
3) მეთოდი ეფუძნება აჩქარების გეგმის გამოყენებას აბსოლუტურად ხისტი სხეულისთვის.
ნახვა:ეს სტატია წაკითხულია 11766 ჯერ
Pdf აირჩიეთ ენა... რუსული უკრაინული ინგლისური
მთელი მასალა გადმოწერილია ზემოთ, ენის შერჩევის შემდეგ
სიბრტყე-პარალელური ან ხისტი სხეულის სიბრტყე მოძრაობა არის მოძრაობა, რომლის დროსაც სხეულის ყველა წერტილი მოძრაობს სიბრტყეებში, რომლებიც პარალელურად არიან რაიმე ფიქსირებული სიბრტყის (ფუძის) პარალელურად.
აბსოლუტურად ხისტი სხეულის სიბრტყის მოძრაობის შესწავლა დაიყვანება სიბრტყე ფიგურის ერთი მონაკვეთის შესწავლით, რომელიც განისაზღვრება სამი წერტილის მოძრაობით, რომლებიც არ დევს იმავე სწორ ხაზზე.
სხეულის ბრუნვის კუთხის მითითებით სწორი ხაზის ირგვლივ, რომელიც გადის A ბოძზე მონაკვეთის სიბრტყის პერპენდიკულარულად, ვიღებთ სიბრტყე-პარალელური მოძრაობის კანონს.
ხისტი სხეულის სიბრტყე-პარალელური მოძრაობა შედგება მთარგმნელობითი მოძრაობისგან, რომლის დროსაც სხეულის წერტილები მოძრაობენ პოლუსთან ერთად და ბრუნვითი მოძრაობისაგან ბოძზე.
თვითმფრინავის სხეულის მოძრაობის ძირითადი კინემატიკური მახასიათებლები:
- პოლუსის მთარგმნელობითი მოძრაობის სიჩქარე და აჩქარება,
- ბოძის გარშემო ბრუნვის მოძრაობის კუთხური სიჩქარე და კუთხური აჩქარება.
ბრტყელი ფიგურის თვითნებური წერტილის ტრაექტორია განისაზღვრება წერტილიდან A პოლუსამდე მანძილით და ბოძის გარშემო ბრუნვის კუთხით.
სიბრტყე ფიგურაზე წერტილების სიჩქარის განსაზღვრა
სიჩქარე თვითნებური წერტილის ტოლია წერტილის სიჩქარის გეომეტრიული ჯამი, რომელიც აღებულია პოლუსად და ამ წერტილის ბრუნვის სიჩქარე მის ბრუნვის მოძრაობაში ბოძთან ერთად სხეულთან ერთად.
სიჩქარის სიდიდე და მიმართულება გვხვდება შესაბამისი პარალელოგრამის აგებით.
მყისიერი სიჩქარის ცენტრი (IVC)
მყისიერი სიჩქარის ცენტრი
(MCS) - წერტილი, რომლის სიჩქარე მოცემულ დროს არის ნული. MCS ითვლება პოლუსად.
- სხეულის თვითნებური წერტილის სიჩქარე, რომელიც ეკუთვნის ბრტყელ ფიგურას, უდრის მის ბრუნვის სიჩქარეს მყისიერი ცენტრის გარშემო. თვითნებური A წერტილის სიჩქარის მოდული უდრის სხეულის კუთხური სიჩქარის ნამრავლს სეგმენტის სიგრძით წერტილიდან MCS-მდე. ვექტორი მიმართულია სეგმენტის პერპენდიკულურად წერტილიდან MCS-მდე სხეულის ბრუნვის მიმართულებით.
- სხეულის წერტილების სიჩქარის მოდულები პროპორციულია მათი მანძილისა MCS-მდე
მყისიერი სიჩქარის ცენტრის განსაზღვრის შემთხვევები
- თუ სხეულის ერთი წერტილის სიჩქარე და სხეულის ბრუნვის კუთხური სიჩქარე ცნობილია, მაშინ MVC (P)-ის საპოვნელად საჭიროა წერტილის სიჩქარის ვექტორი ბრუნვის მიმართულებით 90 0-ით და გამოსახოთ AP სეგმენტი ნაპოვნი სხივზე
- თუ სხეულის ორი წერტილის სიჩქარე პარალელურია და პერპენდიკულარულია იმ წრფეზე, რომელიც გადის ამ წერტილებში, მაშინ MCS მდებარეობს ამ ხაზის გადაკვეთის წერტილში და ხაზი, რომელიც აკავშირებს სიჩქარის ვექტორების ბოლოებს.
- თუ სხეულის ორი წერტილის სიჩქარის მიმართულებები ცნობილია და მათი მიმართულებები არ არის პარალელური, მაშინ MCS განლაგებულია ამ წერტილების სიჩქარეებზე გამოყვანილი პერპენდიკულარების გადაკვეთის P წერტილში.
- თუ ბორბალი მოძრაობს სტაციონარულ ზედაპირზე ცურვის გარეშე, მაშინ MCS (P) მდებარეობს ბორბლის სტაციონარული ზედაპირთან შეხების ადგილზე.
2 და 3 შემთხვევებში შესაძლებელია გამონაკლისები (მყისიერი წინსვლა ან მყისიერი დასვენება).
რთული წერტილის მოძრაობა
რთული წერტილის მოძრაობა - მოძრაობა, რომელშიც წერტილი ერთდროულად მონაწილეობს რამდენიმე მოძრაობაში.
შედარებითი მოძრაობა - მოძრაობა მოძრავი საცნობარო ჩარჩოს მიმართ.
პორტატული მოძრაობა - მოძრავი საცნობარო სისტემის მოძრაობა (გამტარი საშუალება) წერტილთან ერთად სტაციონარული საცნობარო სისტემის მიმართ.
აბსოლუტური მოძრაობა- წერტილის მოძრაობა ფიქსირებულ მიმართვის ჩარჩოსთან მიმართებაში
წერტილის აბსოლუტური მოძრაობა რთული მოძრაობაა, რადგან შედგება ფარდობითი და მთარგმნელობითი მოძრაობებისაგან.
კომპლექსურ მოძრაობაში წერტილის აბსოლუტური სიჩქარე უდრის მისი ფარდობითი და პორტატული სიჩქარის გეომეტრიულ ჯამს.
წერტილოვანი აჩქარებების განსაზღვრა
წერტილის აბსოლუტური აჩქარება უდრის სამი ვექტორის გეომეტრიულ ჯამს: ფარდობითი აჩქარება, რომელიც ახასიათებს ფარდობითი სიჩქარის ცვლილებას ფარდობით მოძრაობაში; პორტატული აჩქარება, რომელიც ახასიათებს პორტატულ მოძრაობაში წერტილის გადასატანი სიჩქარის ცვლილებას და კორიოლისის აჩქარება, რომელიც ახასიათებს პორტატული მოძრაობის წერტილის ფარდობითი სიჩქარის ცვლილებას და პორტატული სიჩქარის ფარდობით მოძრაობაში.
წერტილის კორიოლისის აჩქარება არის გადამცემი გარემოს კუთხური სიჩქარის და წერტილის ფარდობითი სიჩქარის ორმაგი ვექტორული ნამრავლი.
ფორმატი: pdf
ენა: რუსული, უკრაინული
აურზაური მექანიზმის გაანგარიშების მაგალითი
სტიმულატორის გაანგარიშების მაგალითი. განხორციელდა მასალის არჩევა, დასაშვები ძაბვის გამოთვლა, შეხებისა და მოღუნვის სიძლიერის გამოთვლა.
სხივის მოღუნვის პრობლემის გადაჭრის მაგალითი
მაგალითში აშენდა განივი ძალებისა და მოღუნვის მომენტების დიაგრამები, აღმოჩნდა საშიში მონაკვეთი და შეირჩა I-სხივი. პრობლემამ გააანალიზა დიაგრამების აგება დიფერენციალური დამოკიდებულებების გამოყენებით და ჩაატარა სხივის სხვადასხვა ჯვრის მონაკვეთების შედარებითი ანალიზი.
ლილვის ბრუნვის პრობლემის გადაჭრის მაგალითი
ამოცანაა შეამოწმოთ ფოლადის ლილვის სიმტკიცე მოცემულ დიამეტრზე, მასალასა და დასაშვებ სტრესზე. ამოხსნის დროს აგებულია ბრუნვის, ათვლის ძაბვისა და გადახვევის კუთხეების დიაგრამები. ლილვის საკუთარი წონა არ არის გათვალისწინებული
ღეროს დაძაბულობა-შეკუმშვის პრობლემის გადაჭრის მაგალითი
ამოცანაა შეამოწმოთ ფოლადის ზოლის სიმტკიცე მითითებულ დასაშვებ სტრესებზე. ამოხსნის დროს აგებულია გრძივი ძალების, ნორმალური ძაბვისა და გადაადგილების დიაგრამები. ჯოხის საკუთარი წონა არ არის გათვალისწინებული
კინეტიკური ენერგიის შენარჩუნების თეორემის გამოყენება
პრობლემის გადაჭრის მაგალითი მექანიკური სისტემის კინეტიკური ენერგიის კონსერვაციის თეორემის გამოყენებით
წერტილის სიჩქარისა და აჩქარების განსაზღვრა მოძრაობის მოცემული განტოლებების გამოყენებით
პრობლემის გადაჭრის მაგალითი წერტილის სიჩქარისა და აჩქარების დასადგენად მოძრაობის მოცემული განტოლებების გამოყენებით
ხისტი სხეულის წერტილების სიჩქარისა და აჩქარების განსაზღვრა სიბრტყე-პარალელური მოძრაობისას
პრობლემის გადაჭრის მაგალითი ხისტი სხეულის წერტილების სიჩქარისა და აჩქარების დასადგენად სიბრტყე-პარალელური მოძრაობის დროს
ძალების განსაზღვრა ბრტყელი ფერმის გისოსებში
ბრტყელი ფერმის ღეროებში ძალების განსაზღვრის პრობლემის გადაჭრის მაგალითი რიტერის მეთოდისა და კვანძების ჭრის მეთოდის გამოყენებით
ბრტყელი ფიგურის (ან სხეულის სიბრტყეზე მყოფი სხეულის) წერტილების სიჩქარის განსაზღვრის კიდევ ერთი მარტივი და ვიზუალური მეთოდი ეფუძნება სიჩქარის მყისიერი ცენტრის კონცეფციას.
მყისიერი სიჩქარის ცენტრი (IVC) არის ბრტყელი ფიგურის წერტილი, რომლის სიჩქარე დროის მოცემულ მომენტში არის ნული.
თუ ფიგურა მოძრაობს არაპროგრესულად, მაშინ ასეთი წერტილი დროის თითოეულ მომენტში ტარსებობს და უფრო მეტიც, ერთადერთია. ნება მომენტში ტქულები ადა INფიგურის სიბრტყეებს აქვთ სიჩქარეები და , ერთმანეთის არაპარალელური (ნახ. 2.21.). შემდეგ მიუთითეთ რ, წევს პერპენდიკულარების გადაკვეთაზე აჰვექტორამდე და ბბვექტორამდე და იქნება მყისიერი სიჩქარის ცენტრი, ვინაიდან .
სურათი 2.21
სინამდვილეში, თუ , მაშინ სიჩქარის პროექციის თეორემის მიხედვით, ვექტორი უნდა იყოს პერპენდიკულურიც და AR(მას შემდეგ) და VR(რადგან) რაც შეუძლებელია. ამავე თეორემიდან ირკვევა, რომ ფიგურის არცერთ სხვა წერტილს დროის ამ მომენტში არ შეიძლება ჰქონდეს ნულის ტოლი სიჩქარე.
თუ ახლა იმ მომენტში ტმიიღეთ წერტილი რბოძის უკან. შემდეგ წერტილის სიჩქარე ანება
და ასე შემდეგ ფიგურის ნებისმიერი წერტილისთვის.
აქედან გამომდინარეობს ისიც, რომ და , მაშინ
| = , | (2.54) |
იმათ. რა ბრტყელი ფიგურის წერტილების სიჩქარე პროპორციულია მათი დაშორების მყისიერი სიჩქარის ცენტრიდან.
მიღებული შედეგები იწვევს შემდეგ დასკვნებს:
1. სიჩქარის მყისიერი ცენტრის დასადგენად, თქვენ მხოლოდ უნდა იცოდეთ სიჩქარის მიმართულებები, მაგალითად, და სიბრტყე ფიგურის ორი წერტილი A და B.
2. ბრტყელი ფიგურის ნებისმიერი წერტილის სიჩქარის დასადგენად, თქვენ უნდა იცოდეთ ფიგურის ნებისმიერი A წერტილის სიჩქარის სიდიდე და მიმართულება და მისი მეორე B წერტილის სიჩქარის მიმართულება.
3. კუთხური სიჩქარე ბრტყელი ფიგურა დროის თითოეულ მომენტში ტოლია ფიგურის რომელიმე წერტილის სიჩქარის თანაფარდობასთან მის დაშორებაზე სიჩქარის მყისიერი ცენტრიდან P:
განვიხილოთ MCS-ის განსაზღვრის რამდენიმე განსაკუთრებული შემთხვევა, რომელიც დაგეხმარებათ თეორიული მექანიკის ამოხსნაში.
1. თუ სიბრტყე-პარალელური მოძრაობა ხორციელდება ერთი ცილინდრული სხეულის ზედაპირზე მეორე სტაციონარული სხეულის ზედაპირზე სრიალის გარეშე, მაშინ წერტილი რმოძრავი სხეულის, რომელიც ეხება უძრავ ზედაპირს (ნახ. 2.22), დროის მოცემულ მომენტში, სრიალის არარსებობის გამო, აქვს ნულის ტოლი სიჩქარე და, შესაბამისად, არის სიჩქარის მყისიერი ცენტრი.
სურათი 2.22
2. თუ წერტილების სიჩქარე ადა INბრტყელი ფიგურები ერთმანეთის პარალელურია და ხაზი ABარ არის პერპენდიკულარული (სურ. 2.23, ა), მაშინ სიჩქარის მყისიერი ცენტრი დევს უსასრულობაში და ყველა წერტილის სიჩქარე // . ამ შემთხვევაში, სიჩქარის პროგნოზების თეორემიდან გამომდინარეობს, რომ ე.ი. , ამ შემთხვევაში ფიგურას აქვს მყისიერი მთარგმნელობითი მოძრაობა. რომელიც იძლევა.