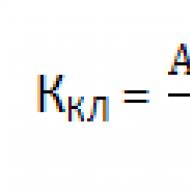Дифференциальное уравнение движения материальной точки. Дифференциальные уравнения динамики. Общее уравнение динамики

Законы механики Галилея – Ньютона

В основу динамики положены законы (аксиомы), являющиеся обобщением практической деятельности человека. Из этих законов логически выводятся различные положения механики. Эти законы были обобщены Галилеем и Ньютоном и сформулированы применительно к материальной точке.

Первый закон Ньютона (закон инерции). Материальная точка, на которую не действуют силы или действует равновесная система сил, обладает способностью сохранять свое состояние покоя или равномерного и прямолинейного движения.

И в первом, и во втором случаях ускорение точки равно нулю, Такое кинематическое состояние точки называется инерциальным .

Все системы отсчета, по отношению к которым выполняется закон инерции, называются инерциальными .

Второй закон Ньютона (основной закон динамики). Ускорение материальной точки относительно инерциальной системы отсчета пропорционально приложенной к точке силе и направлено по этой силе (рис. 1).

Этот закон можно выразить в форме

(1)

где m положительный коэффициент, характеризующий инертные свойства материальной точки, называется массой точки. Масса в классической механике считается величиной постоянной. За единицу массы в системе СИ принят килограмм (кг); – ускорение точки; – приложенная к точке сила.

Рис. 1

Рис. 2

Массу обычно определяют по силе тяготения и ускорению свободного падения у поверхности Земли. Согласно (1), имеем

Третий закон Ньютона (закон о равенстве сил действия и противодействия). Силы взаимодействия двух материальных точек равны по величине и противоположны по направлению (рис. 2), т.е.

Четвертый закон (закон независимости действия сил). При одновременном действии нескольких сил материальная точка приобретает ускорение, равное геометрической сумме тех ускорений, которые она приобрела бы под действием каждой из этих сил в отдельности. Таким образом, приложенные к материальной точке силы действуют на нее независимо друг от друга.

Пусть к материальной точке приложена система сил то, согласно второму закону Ньютона, ускорение от действия каждой силы определяется по выражению (1):

Ускорение при одновременном действии всех сил

(3)

Суммируя (2) и используя (3), получаем основное уравнение динамики точки:

Но такое же ускорение точка приобретает и под действием одной силы

Так как система сил и сила сообщают точке одно и то же ускорение, то эта система сил и сила эквивалентны.

Дифференциальные уравнения движения материальной точки

3.1.2.1. Дифференциальные уравнения движения свободной точки

Рис. 3

Пусть на свободную материальную точку действует система сил, имеющая равнодействующую см. рис. 3. Тогда, согласно основному закону динамики,

(4)

Ускорение точки может быть представлено в виде , поэтому равенство (4) принимает вид:

. (5)

Уравнение (5) – векторное дифференциальное уравнение движения материальной точки. Если его спроектировать на оси декартовой системы координат, то получатся дифференциальные уравнения движения материальной точки в проекциях на эти оси:

При движении точки в плоскости Oxy система уравнений (6) принимает вид:

При движении точки по прямой вдоль оси Ox получаем одно дифференциальное уравнение движения:

Спроектировав равенство (5) на естественные оси координат, получим дифференциальные уравнения движения точки в проекциях на естественные оси координат:

1.2.2. Дифференциальные уравнения движения несвободной точки

Несвободную точку на основании принципа освобождаемости от связей можно превратить в свободную, заменив действие связей их реакциями. Пусть – равнодействующая реакций связей, тогда основное уравнение динамики точки примет вид:

(7)

Спроектировав (7) на оси декартовой системы координат, получим дифференциальные уравнения движения несвободной точки в проекциях на эти оси:

Для решения задач к этим уравнениям надо добавить еще уравнения связей.

Дифференциальные уравнения движения точки в проекциях на естественные оси координат:

1.2.3. Дифференциальные уравнения относительного движения точки

Основное уравнение динамики точки справедливо для инерциальной системы отсчета, где ускорение является абсолютным. Согласно теореме Кориолиса абсолютное ускорение

где – ускорение переносного движения; – относительное ускорение точки по отношению к подвижной системе координат; – ускорение Кориолиса.

Подставив выражение абсолютного ускорения в основное уравнение динамики точки, получим

Введем обозначения: – переносная сила инерции; – кориолисова сила инерции.

Тогда уравнение (9) принимает вид

(10)

Полученное равенство выражает динамическую теорему Кориолиса.

Теорема Кориолиса . Относительное движение материальной точки можно рассматривать как абсолютное, если к действующим на точку силам присоединить переносную и кориолисову силы инерции.

Рассмотрим случай относительного равновесия точки Тогда и ускорение Кориолиса Подставив эти значения в уравнение (10), получим условие относительного равновесия точки:

Чтобы основной закон динамики для относительного движения точки совпадал с основным законом ее абсолютного движения, необходимо выполнение условий:

Это условие выполняется, если подвижная система координат движется поступательно прямолинейно и равномерно По отношению к данным системам отсчета, как и по отношению к неподвижным, при будет выполняться закон инерции. Поэтому все системы отсчета, движущиеся поступательно, прямолинейно и равномерно, а также покоящиеся, являются инерциальными .

Так как законы динамики одинаковы во всех инерциальных системах отсчета, то во всех этих системах механические явления протекают совершенно одинаково, если за начало отсчета принято одно и то же событие. Отсюда следует принцип относительности классической механики.

Принцип относительности классической механики. Никакими механическими опытами нельзя обнаружить инерциальное движение системы отсчета, участвуя вместе с ней в этом движении.

НЕВЯЗКОЙ ЖИДКОСТИ

В данном параграфе установим общие закономерности движения невязкой жидкости. Для этого в потоке невязкой жидкости выделим элементарный объем в виде параллелепипеда с ребрами dx, dy, dz, параллельными координатным осям (рис.4.4).

Рис. 4.4. Схема к выводу дифференциальных уравнений

движения невязкой жидкости

На массу жидкости в объеме параллелепипеда, равную действуют массовые силы, пропорциональные массе, и поверхностные силы давления окружающей жидкости, распределенные по граням параллелепипеда, перпендикулярные к ним и пропорциональные площадям соответствующих граней.

Обозначим через плотность распределения равнодействующей массовых сил и через , - ее проекции на соответствующие оси координат. Тогда проекция на направление ОХ массовых сил, действующих на выделенную массу жидкости, равна .

Обозначим через р - давление в произвольной точке с координатами x, y, z, являющейся одной из вершин параллелепипеда. Пусть это будет точка А на рис.4.4.

В силу сплошности жидкости и непрерывности функции давления р = f (x, y, z, t) в точке В с координатами (х + dx, y, z) давление будет равно с точностью до бесконечно малых второго порядка.

Разность давлений равна и будет одинаковой для любой пары выбранных на гранях точек с одинаковыми координатами у и z.

Проекция на ось ОХ результирующей силы давления равна . Запишем уравнение движения в направлении оси ОХ

или после деления на массу получим

. (4.15)

Аналогично получим уравнения движения в направлении осей OY и OZ. Тогда система дифференциальных уравнений движения невязкой жидкости имеет вид

(4.16)

Эти дифференциальные уравнения были впервые получены Л. Эйлером в1755 г.

Члены этих уравнений представляют собой соответствующие ускорения, а смысл каждого из уравнений заключается в следующем: полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления.

Уравнения Эйлера в таком виде справедливы как для несжимаемой, так и для сжимаемой жидкости, а также для случая, когда наряду с силой тяжести действуют другие массовые силы при относительном движении жидкости. При этом в величины R x , R y и R z должны войти компоненты ускорения переносного (или поворотного) движения. Так как при выводе уравнений (4.6) не накладывались условия стационарности движения, то они справедливы и для неустановившегося движения.

Учитывая, что для неустановившегося движения компоненты (проекции) скорости V являются функциями времени, можно записать ускорение выделенной массы жидкости в развернутом виде:

Так как уравнения Эйлера (4.16) можно переписать в виде

. (4.18)

Для случая покоящейся жидкости уравнения (4.16) совпадают с дифференциальными уравнениями равновесия жидкости (2.5).

В задачах динамики жидкости массовые силы обычно считаются заданными (известными). Неизвестными являются функции давления
р = f (x,y,z,t), проекции скорости V x = f (x, y, z, t), Y y = f (x, y, z, t),
V z = f (x, y, z, t) и плотность r = f (x, y, z, t), т.е. всего пять неизвестных функций.

Для определения неизвестных переменных используется система уравнений Эйлера. Поскольку число неизвестных превышает число уравнений к системе Эйлера добавляют уравнение неразрывности и уравнение состояния среды.

Для несжимаемой жидкости уравнение состояния p = const и уравнение неразрывности

. (4.19)

Профессором Казанского университета И.С.Громекой в 1881 г. уравнения Эйлера были преобразованы и записаны в иной форме. Рассмотрим уравнения (4.18).

В первом из них вместо и подставим их выражения из (3. 13):

и . (4.20)

Приняв обозначение , можем записать

Аналогично преобразовав два остальных уравнения системы (4.7), получим систему уравнений в форме, данной Громекой

(4.23)

Если действующие на жидкость массовые силы обладают потенциалом, то проекции плотности распределения массовых сил R x , R y , R z представляются частными производными от потенциальной функции П:

DП = R x dx + R y dy + R z dz .(4.25)

Подставив значения R x , R y , R z в систему (4.8), получим систему дифференциальных уравнений движения несжимаемой жидкости под действием сил, имеющих потенциал:

(4.26)

При установившемся движении частные производные составляющих скорости по времени равны нулю:

. (4.27)

Тогда уравнения системы (4.10) примут вид

(4.28)

Умножив каждое из уравнений системы (4.11) на соответствующие проекции элементарного перемещения, равные dx = V x dt; dy = V y dt;
dz = V z dt, и сложим уравнения. Будем иметь

Правую часть полученного выражения можно переписать в виде определителя, т.е.

(4.29)

Если определитель равен нулю, т.е.

(4.30)

. (4.31)

Это уравнение Бернулли для элементарной струйки при установившемся движении невязкой жидкости.

Чтобы привести уравнение (4.14) к виду уравнения Бернулли, полученному в (4.1), определим вид потенциальной функции П для случая, когда действует только одна массовая сила - сила тяжести. В этом случае R x = R y = 0 и R z = - g (ось OZ направлена вверх). Из (4.9) имеем

или . (4.32)

Подставив это выражение П в (4.14), получим

или .

Последнее выражение полностью соответствует уравнению Бернулли (4.4).

Выясним, в каких случаях установившегося движения невязкой несжимаемой жидкости справедливо уравнение Бернулли или, иначе говоря, в каких случаях определитель в правой части уравнения (4.13) обращается в нуль.

Известно, что определитель равен нулю, если две строки (или два столбца) равны или пропорциональны друг другу или если одна из его строк или один из столбцов равны нулю. Рассмотрим эти случаи последовательно.

А. Пропорциональны члены первой и третьей строк, т.е. уравнение Бернулли справедливо, если

Это условие выполняется на линиях тока (3.2).

Б. Пропорциональны члены первой и второй строк, т.е. уравнение Бернулли справедливо, если

Это условие выполняется на вихревых линиях (3.16).

В. Пропорциональны члены второй и третьей строк:

. (4.16)

Тогда ω x = a V x ; ω y = a V y ; ω z = a V z .

Проектируя уравнение (1) на координатные оси и учитывая зависимости задаваемых сил от координат, скоростей и времени, получим дифференциальные уравнения динамики точки. Так, для декартовых координат имеем:

Дифференциальные уравнения движения в цилиндрической системе координат будут иметь вид

;

В заключение приведем дифференциальные уравнения динамики точки в проекциях на оси натурального триэдра; эти уравнения бывают особенно удобны в тех случаях, когда известна траектория движения точки. Проектируя уравнение (3.1) на касательную, главную нормаль и бинормаль к траектории, получаем

, ,

Рассмотрим теперь на примере уравнений динамики точки в декартовых координатах (3.2) постановку и процесс решения задач динамики точки. Существуют две основные задачи динамики точки: прямая и обратная. Первая задача динамики (прямая) состоит в следующем: дано движение точки, обладающей массой , т. е. заданы функции

требуется найти силы, вызывающие это движение. Решение этой задачи не представляет затруднении. Согласно уравнениям (3.1) и (3.3) находим проекции для чего дважды дифференцируем заданные функции (3.3).

, , (3.4)

Выражения (3.4) представляют проекции равнодействующей всех сил, действующих на точку; часть сил (или часть проекций)могут быть известными, остальные (но не более трёх проекций) найдутся из уравнений (3.4). Эту задачу можноформально привести к решению задачи статики, если переписать уравнение (3.1) в виде

Здесь - сила инерции точки, проекции которой на оси х, у, z равны выражениям (3.3) с противоположными знаками. Формальное сведение задачи динамики к задаче статики при помощи введения сил инерции, которое довольно часто практикуется в задачах механики, носит название метода кинетостатики.

Вторая (обратная) задача динамики точки ставится следующим образом: на точку массы т, положение и вектор скорости которой в начальный момент времени известны, действуют заданные силы; требуется найти движение этой точки (ее координаты х,у,z) как функции времени. Так как правые части уравнений (2) -проекции сил на оси х, у, z- являются известными функциями координат, их первых производных и времени, то для получения требуемого результата надо проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка. Аналитическое решение такой задачи оказывается возможным лишь в отдельных частных случаях. Однако численные методы позволяют решить задачу с практически любой необходимой степенью точности. Предположим, что мы проинтегрировали систему дифференциальных уравнений (3.2) и нашли выражения для координат х, у, z в функции времени. Так как система (3.2) имеет шестой порядок, то при интегрировании ее появятся шесть произвольных постоянных и мы получим следующие выражения для координат:

Для определения постоянных (i = 1, 2,... 6) в этом решении следует обратиться к начальным условиям задачи. Записывая поставленные условия применительно к декартовым координатам, имеем при t = 0

Подставляя в найденное выражение (3.5) первую группу начальных условий (3.6) при t =0, получаем три уравнения, связывающие постоянные интегрирования:

Недостающие три соотношения находятся следующим образом: дифференцируем уравнения движения (3.5) по времени и подставляем в полученные выражения вторую группу начальных условий (3.6) при t = 0; имеем

Решая теперь совместно эти шесть уравнений, получим искомые значения шести произвольных постоянных интегрирования (i = 1, 2,... 6), подставляя которые в уравнения движения (3.5), находим окончательное решение задачи.

При составлении дифференциальных уравнений движения точки для конкретного случая следует, прежде всего, оценить действия различных факторов: учесть основные силы и отбросить второстепенные. При решении различных технических задач часто пренебрегают силами сопротивления воздуха и силами сухого трения; так, например, поступают при вычислении собственных частот колебательных систем, на значения которых упомянутые силы оказывают незначительное влияние. Если тело движется вблизи поверхности земли, то его силу тяжести считают постоянной, а поверхности земли - плоской; при удалении от поверхности земли па расстояния, сравнимые с ее радиусом, необходимо уже принимать во внимание изменение силы тяжести с высотой, поэтому в таких задачах используется закон тяготения Ньютона.

Нельзя пренебрегать силой сопротивления воздуха при больших скоростях движения тела; в этом случае обычно принимают квадратичный закон сопротивления (сила сопротивления считается пропорциональной квадрату скорости движения тела).

(3.6)

Здесь - скоростной напор, ρ – плотность среды, в которой движется точка, - коэффициент сопротивления, - характерный поперечный размер. Однако, как будет показано ниже, в некоторых задачах необходимо учитывать внутреннее трение в жидкости (в газе), что приводит к более общей формуле для определения силы сопротивления

Если движение тела происходит в вязкой среде, то и при небольших скоростях движения надо учитывать силу сопротивления, однако в этой задаче достаточно считать ее пропорциональной первой степени скорости.

Пример. Рассмотрим задачу о прямолинейном движении точки в среде с сопротивлением, сила сопротивления задана выражением (3.6). Начальная скорость точки - , конечная - . Надо определить среднюю скорость движения на заданном интервале скоростей. Из формулы (3.2) имеем

(3.7)

Это дифференциальное уравнение с разделяющимися переменными, решение которого может быть представлено в виде

решение которого запишется в виде

(3.8)

Для определения пройденного расстояния перейдём к новым координатам, для этого умножим левую и правую части уравнения (3.7) на ; при этом заметим, что

тогда и здесь получаем дифференциальное уравнение с разделяющимися переменными

решение которого может быть представлено в виде

(3.9)

Из формул (3.8) и (3.9) получаем выражение для средней скорости

Для средняя скорость равна .

Но если положить , то нетрудно увидеть, что в этом случае и , то есть движущееся тело никогда не остановится, что, во-первых, противоречит здравому смыслу, а во-вторых неясно чему будет равна средняя скорость. Чтобы определить возьмём левые интегралы в пределах от до бесконечно малого ε, тогда получим

Используя основной закон динамики и формулы для ускорения МТ при различных способах задания движения, можно получить дифференциальные уравнения движения как свободной, так и несвободной материальной точки. При этом для несвободной материальной точки ко всем приложенным к МТ активным (заданным) силам надо добавить на основании аксиомы связей (принципа освобождаемости) силы пассивные (реакции связи).

Пусть – равнодействующая системы сил (активных и реакций), действующих на точку.

На основании второго закона динамики

с учетом соотношения, определяющего ускорение точки при векторном способе задания движения: ,

получим дифференциальное уравнение движения МТ постоянной массы в векторной форме:

Спроектировав соотношение (6) на оси декартовой системы координат Oxyz и использовав соотношения, определяющие проекции ускорения на оси декартовой системы координат:

получим дифференциальные уравнения движения материальной точки в проекциях на эти оси:

Спроектировав соотношение (6) на оси естественного трехгранника () и использовав соотношения, определяющие формулы для ускорения точки при естественном способе задания движения:

получим дифференциальные уравнения движения материальной точки в проекциях на оси естественного трехгранника:

Аналогично можно получить дифференциальные уравнения движения материальной точки в других системах координат (полярной, цилиндрической, сферической и т. д.).

С помощью уравнений (7)-(9) ставятся и решаются две основные задачи динамики материальной точки.

Первая (прямая) задача динамики материальной точки :

зная массу материальной точки и заданные тем или иным способом уравнения или кинематические параметры ее движения, необходимо найти действующие на материальной точки силы.

Например, если заданы уравнения движения материальной точки в декартовой системе координат:

то проекции на оси координат силы , действующей на МТ, определятся после использования соотношений (8):

Зная проекции силы на координатные оси, легко определить модуль силы и направляющие косинусы углов, которые составляет сила с осями декартовой системы координат.

Для несвободной МТ обычно необходимо еще, зная действующие на нее активные силы, определить реакции связи.

Вторая (обратная) задача динамики материальной точки:

зная массу точки и действующие на нее силы, необходимо определить уравнения или кинематические параметры ее движения при определенном способе задания движения.

Для несвободной материальной точки обычно необходимо, зная массу материальной точки и действующие на нее активные силы, определить уравнения или кинематические параметры ее движения и реакции связи.

Силы, приложенные к точке, могут зависеть от времени, положения материальной точки в пространстве и от скорости ее движения, т. е.

Рассмотрим решение второй задачи в декартовой системе координат. Правые части дифференциальных уравнений движения (8) в общем случае содержат функции времени, координат, их производных по времени:

Для того, чтобы найти уравнения движения МТ в декартовых координатах, необходимо дважды проинтегрировать систему трех обыкновенных дифференциальных уравнений второго порядка (10), в которых неизвестными функциями являются координаты движущейся точки, а аргументом – время t. Из теории обыкновенных дифференциальных уравнений известно, что общее решение системы трех дифференциальных уравнений второго порядка содержит шесть произвольных постоянных:

где C g , (g = 1,2,…,6) – произвольные постоянные.

Продифференцировав соотношения (11) по времени, определим проекции скорости МТ на координатные оси:

В зависимости от значений постоянных C g , (g =1,2,…,6) уравнения (11) описывают целый класс движений, который могла бы совершить МТ под действием данной системы сил.

Действующие силы определяют только ускорение МТ, а скорость и положение МТ на траектории зависят еще от скорости, которую сообщили МТ в начальный момент, и от начального положения МТ.

Для выделения конкретного вида движения МТ (т. е. чтобы сделать вторую задачу определенной) надо дополнительно задать условия, позволяющие определить произвольные постоянные. В качестве таких условий задают начальные условия, т. е. в какой-то определенный момент времени, принимаемый за начальный, задаются координаты движущейся МТ и проекции ее скорости:

где – значения координат материальной точки и их производных в начальный момент времени t=0.

Используя начальные условия (13), формулы (12) и (11), получаем шесть алгебраических уравнений для определения шести произвольных постоянных:

Из системы (14) можно определить все шесть произвольных постоянных:

. (g = 1,2,…,6)

Подставляя найденные значения C g , (g = 1,2,…,6) в уравнения движения (11), находим решения второй задачи динамики в виде закона движения точки.

РАЗДЕЛ 3. ДИНАМИКА.

Динамика Материальное тело - тело, имеющее массу.

Материальная точка

Материальными

а - б в -

Инертность

Масса тела

Сила -

. а - б - - сила тяги электровоза; в - -

Система Инерциальная

Движение Пространство Время

Система

ТЕМА 1

Первый закон (закон инерции).

Изолированная

Например: - вес тела, -

- начальная скорость).

Второй закон (основной закон динамики).

Математически этот закон выражается векторным равенством

При ускорения - движение точки - равнопеременное (рис. 5: а - движение - замедленное, ; б - движение - ускоренное, . - масса точки, - вектор ускорения, - вектор силы, - вектор скорости).

При - точка движется равномерно и прямолинейно либо при - покоится (закон инерции). Второй закон позволяет установить связь между массой тела , находящегося вблизи земной поверхности, и его весом , , где - ускорение свободного падения.

Третий закон (закон равенства действия и противодействия).

Две материальные точки действуют друг на друга с силами, равными по величине и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.

Так как силы приложены к разным точкам, то система сил не является уравновешенной.(рис. 6). В свою очередь - отношение масс взаимодействующих точек обратно пропорционально их ускорениям.

Четвертый закон (закон независимости действия сил).

Ускорение, получаемое точкой при действии на нее одновременно нескольких сил, равно геометрической сумме тех ускорений, которые получила бы точка при действии на нее каждой силы в отдельности.

Пояснение (рис. 7). Равнодействующая сил определяется как . Так как и , то .

Вторая (обратная) задача.

Зная действующие на точку силы, ее массу и начальные условия движения, определить закон движения точки или какие-либо другие ее кинематические характеристики.

Начальные условия движения точки в декартовых осях - это координаты точки , , и проекции начальной скорости на эти оси , и в момент времени, соответствующий началу движения точки и принимаемый равным нулю.

Решение задач этого типа сводится к составлению дифференциальных уравнений (или одного уравнения) движения материальной точки и их последующему решению путем непосредственного интегрирования или с использованием теории дифференциальных уравнений.

ТЕМА 2 . ВВЕДЕНИЕ В ДИНАМИКУ МЕХАНИЧЕСКОЙ СИСТЕМЫ

2.1. Основные понятия и определения

Механической системой или системой материальных точек называют совокупность взаимодействующих между собой материальных точек.

Примеры механических систем:

1. материальное тело, в том числе и абсолютно твердое, как совокупность взаимодействующих материальных частиц; совокупность взаимосвязанных твердых тел; совокупность планет солнечной системы и т. д.

2. Стая летящих птиц не является механической системой, т. к. между птицами нет силового взаимодействия.

Свободная механическая система - система, на движение точек которой не наложено никаких связей. Например: движение планет солнечной системы.

Несвободная механическая система - система, на движение точек которой наложены связи. Например: движение деталей в любом механизме, машине и т. п.

Классификация сил

Классификацию сил, действующих на несвободную механическую систему, можно представить в виде следующей схемы:

Внешние силы - силы, действующие на точки данной механической системы со стороны других систем.

Внутренние - силы взаимодействия между точками одной механической системы.

На произвольную точку системы (рис. 1) действуют: - равнодействующая внешних сил (индекс - первая буква французского слова exterieur - (внешний)); - равнодействующая внутренних сил (индекс - от слова interieur - (внутренний)). Одна и та же сила реакции связи в зависимости от условия задачи может быть как внешней, так и внутренней.

Свойство внутренних сил

и - взаимодействующие точки механической системы (рис. 2). На основании 3-го закона динамики

С другой стороны: . Поэтому главный вектор и главный момент внутренних сил механической системы равны нулю:

РАЗДЕЛ 3. ДИНАМИКА.

ОСНОВНЫЕ ПОНЯТИЯ КЛАССИЧЕСКОЙ МЕХАНИКИ

Динамика - раздел теоретической механики, в котором изучается движение материальных тел (точек) под действием приложенных сил. Материальное тело - тело, имеющее массу.

Материальная точка - материальное тело, различие в движении точек которого является несущественным. Это может быть как тело, размерами которого при его движении можно пренебречь, так и тело конечных размеров, если оно движется поступательно.

Материальными точками называют также частицы, на которые мысленно разбивается твердое тело при определении некоторых его динамических характеристик.

Примеры материальных точек (рис. 1): а - движение Земли вокруг Солнца. Земля - материальная точка; б - поступательное движение твердого тела. Твердое тело - материальная точка, т. к. ; в - вращение тела вокруг оси. Частица тела - материальная точка.

Инертность - свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил.

Масса тела - это скалярная положительная величина, зависящая от количества вещества, содержащегося в данном теле, и определяющая его меру инертности при поступательном движении. В классической механике масса - величина постоянная.

Сила - количественная мера механического взаимодействия между телами или между телом (точкой) и полем (электрическим, магнитным и т. д.). Сила - векторная величина, характеризующаяся величиной, точкой приложения и направлением (линией действия) (рис. 2: - точка приложения, - линия действия силы).

В динамике наряду с постоянными силами имеют место и переменные силы, которые могут зависеть от времени , скорости , расстояния или от совокупности этих величин, т. е.

Примеры таких сил приведены на рис. 3. а - - вес тела, - сила сопротивления воздуха; б - - сила тяги электровоза; в - - сила отталкивания от центра или притяжения к нему.

Система отсчета - система координат, связанная с телом, по отношению к которому изучается движение другого тела. Инерциальная система - система, в которой выполняются первый и второй законы динамики. Это неподвижная система координат либо система, движущаяся равномерно и прямолинейно поступательно.

Движение в механике - это изменение положения тела в пространстве и во времени. Пространство в классической механике трехмерное, подчиняющееся эвклидовой геометрии. Время - скалярная величина, одинаково протекающая в любых системах отсчета.

Система единиц - это совокупность единиц измерения физических величин. Для измерения всех механических величин: достаточно трех основных единиц: единицы длины, времени, массы или силы. Все остальные единицы измерения механических величин - производные от этих. Применяются два типа систем единиц: международная система единиц СИ (или более мелкая - СГС) и техническая система единиц - МкГС.

ТЕМА 1 . ВВЕДЕНИЕ В ДИНАМИКУ МАТЕРИАЛЬНОЙ ТОЧКИ.

1.1. Законы динамики материальной точки (законы Галилея-Ньютона)

Первый закон (закон инерции).

Изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или движется равномерно и прямолинейно до тех пор, пока приложенные силы не заставят ее изменить это состояние.

Движение, совершаемое точкой при отсутствии сил или под действием уравновешенной системы сил, называется движением по инерции.

Например: движение тела по гладкой (сила трения равна нулю) горизонтальной поверхности (рис. 4: - вес тела, - нормальная реакция плоскости). Так как , то .

При тело движется с той же скоростью; при тело покоится (- начальная скорость).